A Linear Approach to Data Poisoning

We investigate the theoretical foundations of data poisoning attacks in machine learning models. Our analysis reveals that the Hessian with respect to the input serves as a diagnostic tool for detecting poisoning, exhibiting spectral signatures that characterize compromised datasets. We use random matrix theory (RMT) to develop a theory for the impact of poisoning proportion and regularisation on attack efficacy in linear regression. Through QR stepwise regression, we study the spectral signatures of the Hessian in multi-output regression. We perform experiments on deep networks to show experimentally that this theory extends to modern convolutional and transformer networks under the cross-entropy loss. Based on these insights we develop preliminary algorithms to determine if a network has been poisoned and remedies which do not require further training.

HessFormer: Hessians at Foundation Scale

Whilst there have been major advancements in the field of first order optimisation of deep learning models, where state of the art open source mixture of expert models go into the hundreds of billions of parameters, methods that rely on Hessian vector products, are still limited to run on a single GPU and thus cannot even work for models in the billion parameter range. We release a software package \textbf{HessFormer}, which integrates nicely with the well known Transformers package and allows for distributed hessian vector computation across a single node with multiple GPUs. Underpinning our implementation is a distributed stochastic lanczos quadrature algorithm, which we release for public consumption. Using this package we investigate the Hessian spectral density of the recent Deepseek $70$bn parameter model.

Compute-Optimal LLMs Provably Generalize Better With Scale

Why do larger language models generalize better? To investigate this question, we develop generalization bounds on the pretraining objective of large language models (LLMs) in the compute-optimal regime, as described by the Chinchilla scaling laws. We introduce a novel, fully empirical Freedman-type martingale concentration inequality that tightens existing bounds by accounting for the variance of the loss function. This generalization bound can be decomposed into three interpretable components: the number of parameters per token, the loss variance, and the quantization error at a fixed bitrate. As compute-optimal language models are scaled up, the number of parameters per data point remains constant; however, both the loss variance and the quantization error decrease, implying that larger models should have smaller generalization gaps. We examine why larger models tend to be more quantizable from an information theoretic perspective, showing that the rate at which they can integrate new information grows more slowly than their capacity on the compute-optimal frontier. From these findings we produce a scaling law for the generalization gap, with bounds that become predictably stronger with scale.

Universal characteristics of deep neural network loss surfaces from random matrix theory

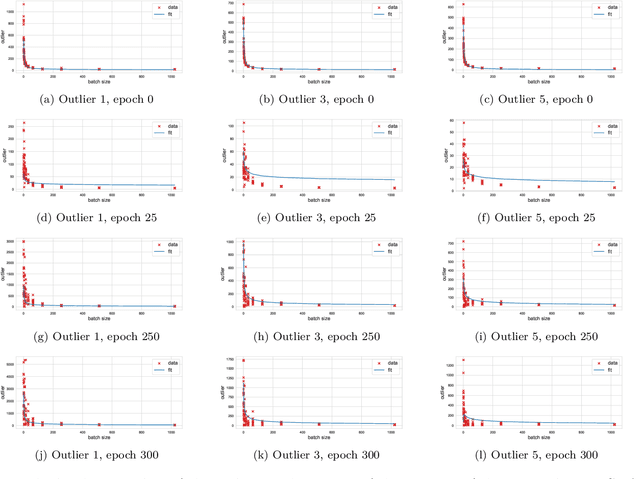
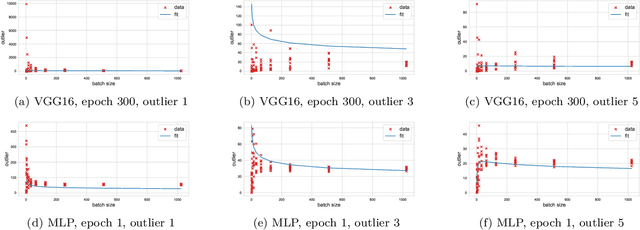
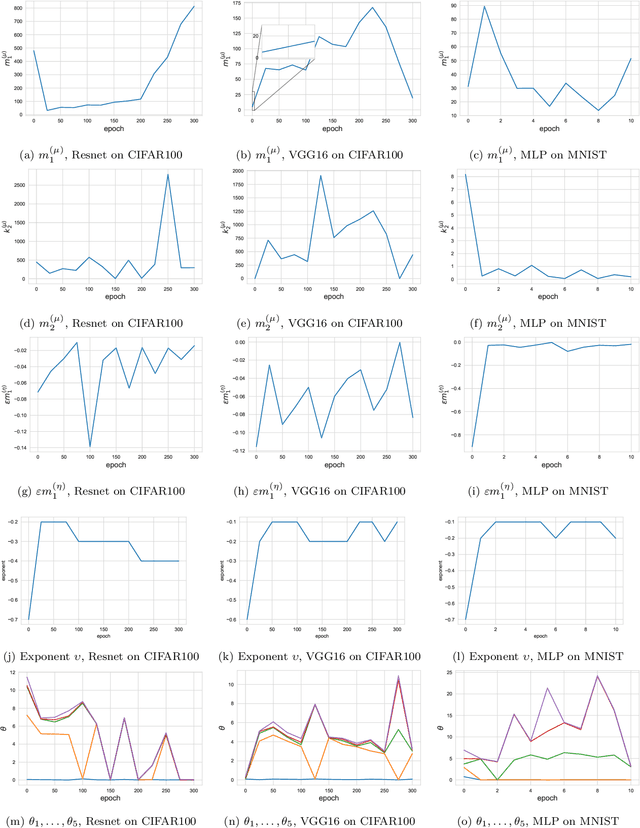
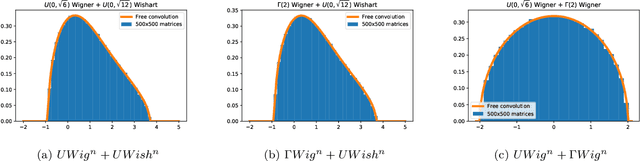
This paper considers several aspects of random matrix universality in deep neural networks. Motivated by recent experimental work, we use universal properties of random matrices related to local statistics to derive practical implications for deep neural networks based on a realistic model of their Hessians. In particular we derive universal aspects of outliers in the spectra of deep neural networks and demonstrate the important role of random matrix local laws in popular pre-conditioning gradient descent algorithms. We also present insights into deep neural network loss surfaces from quite general arguments based on tools from statistical physics and random matrix theory.

Applicability of Random Matrix Theory in Deep Learning

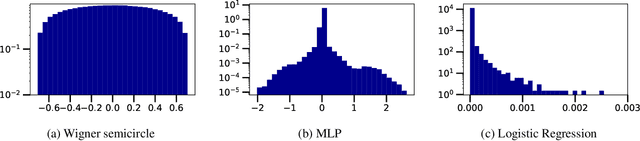
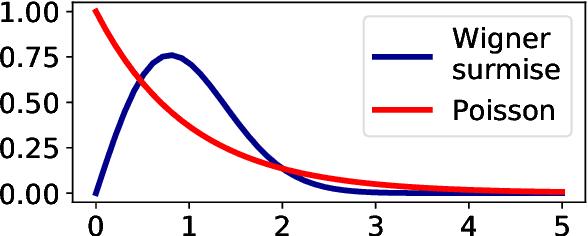
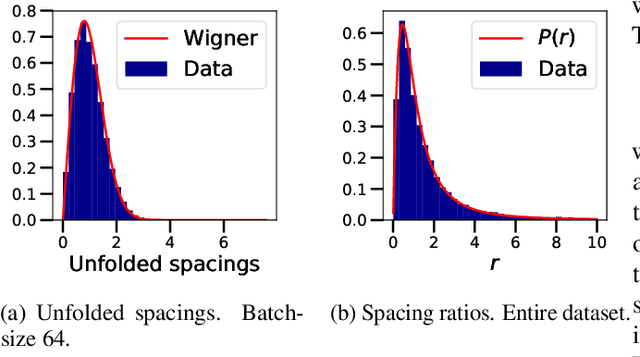
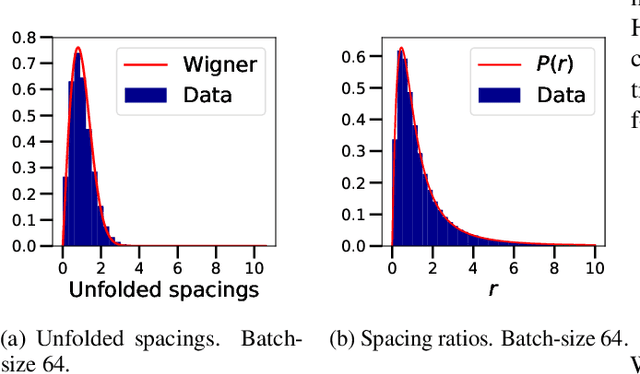
We investigate the local spectral statistics of the loss surface Hessians of artificial neural networks, where we discover excellent agreement with Gaussian Orthogonal Ensemble statistics across several network architectures and datasets. These results shed new light on the applicability of Random Matrix Theory to modelling neural networks and suggest a previously unrecognised role for it in the study of loss surfaces in deep learning. Inspired by these observations, we propose a novel model for the true loss surfaces of neural networks, consistent with our observations, which allows for Hessian spectral densities with rank degeneracy and outliers, extensively observed in practice, and predicts a growing independence of loss gradients as a function of distance in weight-space. We further investigate the importance of the true loss surface in neural networks and find, in contrast to previous work, that the exponential hardness of locating the global minimum has practical consequences for achieving state of the art performance.

Explaining the Adaptive Generalisation Gap

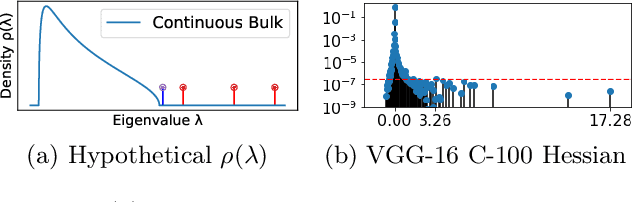
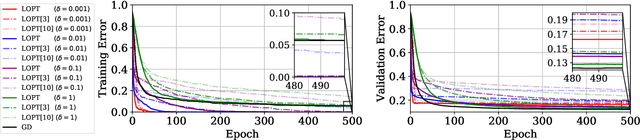
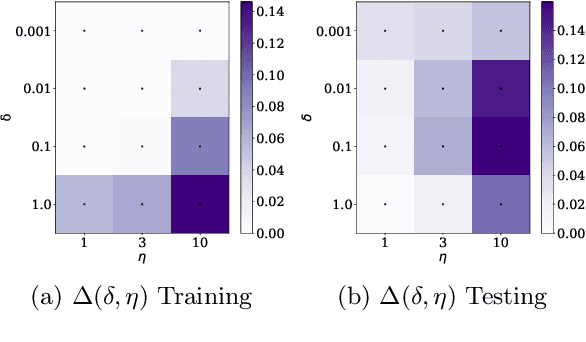
We conjecture that the reason for the difference in generalisation between adaptive and non adaptive gradient methods stems from the failure of adaptive methods to account for the greater levels of noise associated with flatter directions in their estimates of local curvature. This conjecture motivated by results in random matrix theory has implications for optimisation in both simple convex settings and deep neural networks. We demonstrate that typical schedules used for adaptive methods (with low numerical stability or damping constants) serve to bias relative movement towards flat directions relative to sharp directions, effectively amplifying the noise-to-signal ratio and harming generalisation. We show that the numerical stability/damping constant used in these methods can be decomposed into a learning rate reduction and linear shrinkage of the estimated curvature matrix. We then demonstrate significant generalisation improvements by increasing the shrinkage coefficient, closing the generalisation gap entirely in our neural network experiments. Finally, we show that other popular modifications to adaptive methods, such as decoupled weight decay and partial adaptivity can be shown to calibrate parameter updates to make better use of sharper, more reliable directions.

Curvature is Key: Sub-Sampled Loss Surfaces and the Implications for Large Batch Training

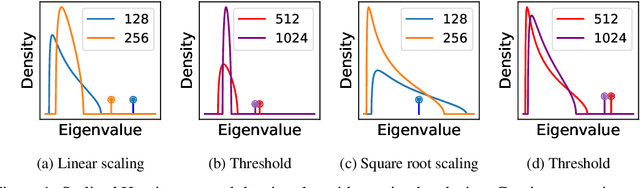
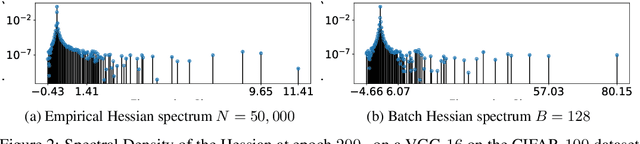
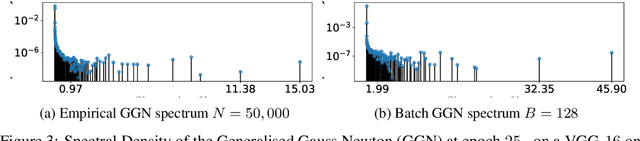
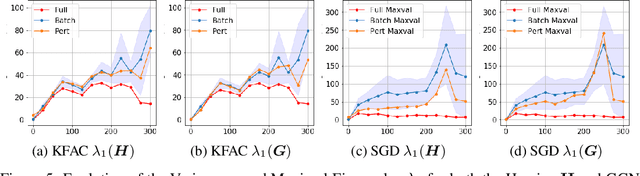
We study the effect of mini-batching on the loss landscape of deep neural networks using spiked, field-dependent random matrix theory. We show that the magnitude of the extremal values of the batch Hessian are larger than those of the empirical Hessian. Our framework yields an analytical expression for the maximal SGD learning rate as a function of batch size, informing practical optimisation schemes. We use this framework to demonstrate that accepted and empirically-proven schemes for adapting the learning rate emerge as special cases of our more general framework. For stochastic second order methods and adaptive methods, we derive that the minimal damping coefficient is proportional to the ratio of the learning rate to batch size. For adaptive methods, we show that for the typical setup of small learning rate and small damping, square root learning rate scalings with increasing batch-size should be employed. We validate our claims on the VGG/WideResNet architectures on the CIFAR-$100$ and ImageNet datasets.

Flatness is a False Friend

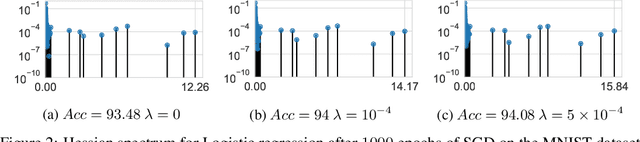
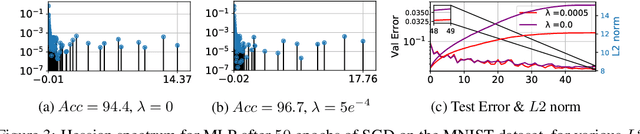
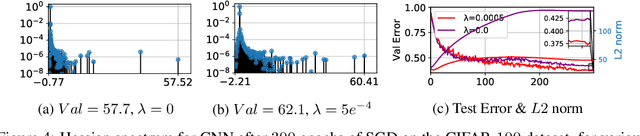
Hessian based measures of flatness, such as the trace, Frobenius and spectral norms, have been argued, used and shown to relate to generalisation. In this paper we demonstrate that for feed forward neural networks under the cross entropy loss, we would expect low loss solutions with large weights to have small Hessian based measures of flatness. This implies that solutions obtained using $L2$ regularisation should in principle be sharper than those without, despite generalising better. We show this to be true for logistic regression, multi-layer perceptrons, simple convolutional, pre-activated and wide residual networks on the MNIST and CIFAR-$100$ datasets. Furthermore, we show that for adaptive optimisation algorithms using iterate averaging, on the VGG-$16$ network and CIFAR-$100$ dataset, achieve superior generalisation to SGD but are $30 \times$ sharper. This theoretical finding, along with experimental results, raises serious questions about the validity of Hessian based sharpness measures in the discussion of generalisation. We further show that the Hessian rank can be bounded by the a constant times number of neurons multiplied by the number of classes, which in practice is often a small fraction of the network parameters. This explains the curious observation that many Hessian eigenvalues are either zero or very near zero which has been reported in the literature.

Beyond Random Matrix Theory for Deep Networks

We investigate whether the Wigner semi-circle and Marcenko-Pastur distributions, often used for deep neural network theoretical analysis, match empirically observed spectral densities. We find that even allowing for outliers, the observed spectral shapes strongly deviate from such theoretical predictions. This raises major questions about the usefulness of these models in deep learning. We further show that theoretical results, such as the layered nature of critical points, are strongly dependent on the use of the exact form of these limiting spectral densities. We consider two new classes of matrix ensembles; random Wigner/Wishart ensemble products and percolated Wigner/Wishart ensembles, both of which better match observed spectra. They also give large discrete spectral peaks at the origin, providing a theoretical explanation for the observation that various optima can be connected by one dimensional of low loss values. We further show that, in the case of a random matrix product, the weight of the discrete spectral component at $0$ depends on the ratio of the dimensions of the weight matrices.

Iterate Averaging Helps: An Alternative Perspective in Deep Learning

Iterate averaging has a rich history in optimisation, but has only very recently been popularised in deep learning. We investigate its effects in a deep learning context, and argue that previous explanations on its efficacy, which place a high importance on the local geometry (flatness vs sharpness) of final solutions, are not necessarily relevant. We instead argue that the robustness of iterate averaging towards the typically very high estimation noise in deep learning and the various regularisation effects averaging exert, are the key reasons for the performance gain, indeed this effect is made even more prominent due to the over-parameterisation of modern networks. Inspired by this, we propose Gadam, which combines Adam with iterate averaging to address one of key problems of adaptive optimisers that they often generalise worse. Without compromising adaptivity and with minimal additional computational burden, we show that Gadam (and its variant GadamX) achieve a generalisation performance that is consistently superior to tuned SGD and is even on par or better compared to SGD with iterate averaging on various image classification (CIFAR 10/100 and ImageNet 32$\times$32) and language tasks (PTB).