Curvature is Key: Sub-Sampled Loss Surfaces and the Implications for Large Batch Training
Paper and Code
Jun 16, 2020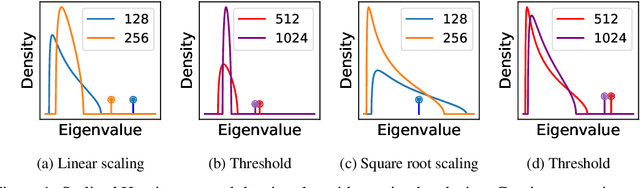
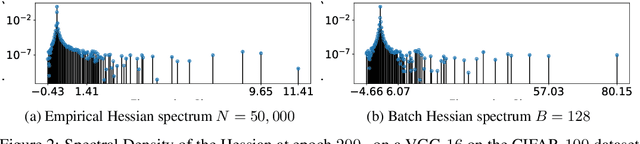
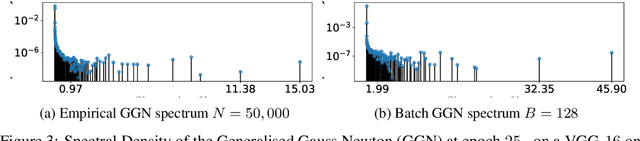
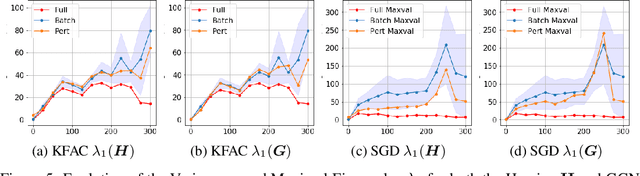
We study the effect of mini-batching on the loss landscape of deep neural networks using spiked, field-dependent random matrix theory. We show that the magnitude of the extremal values of the batch Hessian are larger than those of the empirical Hessian. Our framework yields an analytical expression for the maximal SGD learning rate as a function of batch size, informing practical optimisation schemes. We use this framework to demonstrate that accepted and empirically-proven schemes for adapting the learning rate emerge as special cases of our more general framework. For stochastic second order methods and adaptive methods, we derive that the minimal damping coefficient is proportional to the ratio of the learning rate to batch size. For adaptive methods, we show that for the typical setup of small learning rate and small damping, square root learning rate scalings with increasing batch-size should be employed. We validate our claims on the VGG/WideResNet architectures on the CIFAR-$100$ and ImageNet datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge