Flatness is a False Friend
Paper and Code
Jun 16, 2020
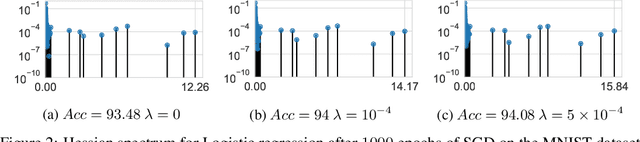
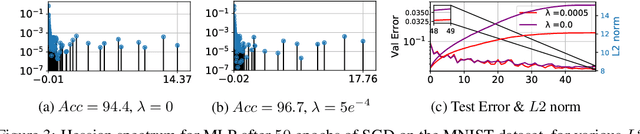
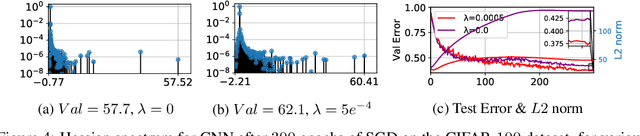
Hessian based measures of flatness, such as the trace, Frobenius and spectral norms, have been argued, used and shown to relate to generalisation. In this paper we demonstrate that for feed forward neural networks under the cross entropy loss, we would expect low loss solutions with large weights to have small Hessian based measures of flatness. This implies that solutions obtained using $L2$ regularisation should in principle be sharper than those without, despite generalising better. We show this to be true for logistic regression, multi-layer perceptrons, simple convolutional, pre-activated and wide residual networks on the MNIST and CIFAR-$100$ datasets. Furthermore, we show that for adaptive optimisation algorithms using iterate averaging, on the VGG-$16$ network and CIFAR-$100$ dataset, achieve superior generalisation to SGD but are $30 \times$ sharper. This theoretical finding, along with experimental results, raises serious questions about the validity of Hessian based sharpness measures in the discussion of generalisation. We further show that the Hessian rank can be bounded by the a constant times number of neurons multiplied by the number of classes, which in practice is often a small fraction of the network parameters. This explains the curious observation that many Hessian eigenvalues are either zero or very near zero which has been reported in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge