Universal characteristics of deep neural network loss surfaces from random matrix theory

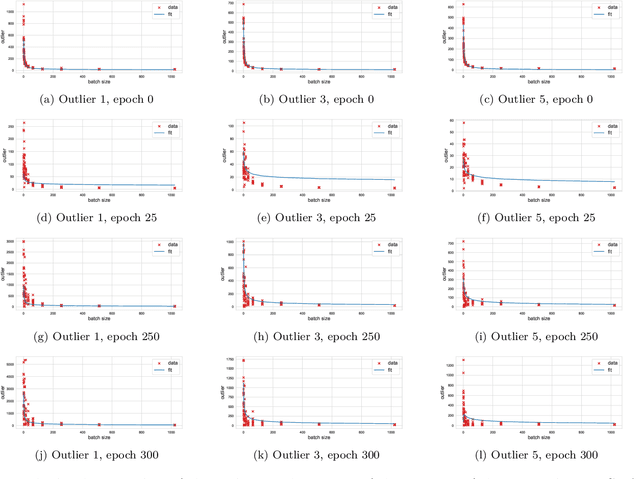
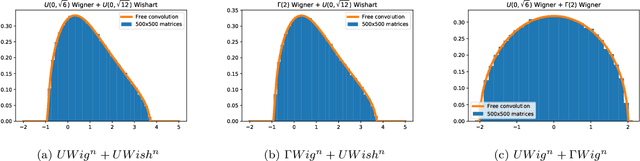
This paper considers several aspects of random matrix universality in deep neural networks. Motivated by recent experimental work, we use universal properties of random matrices related to local statistics to derive practical implications for deep neural networks based on a realistic model of their Hessians. In particular we derive universal aspects of outliers in the spectra of deep neural networks and demonstrate the important role of random matrix local laws in popular pre-conditioning gradient descent algorithms. We also present insights into deep neural network loss surfaces from quite general arguments based on tools from statistical physics and random matrix theory.

Applicability of Random Matrix Theory in Deep Learning

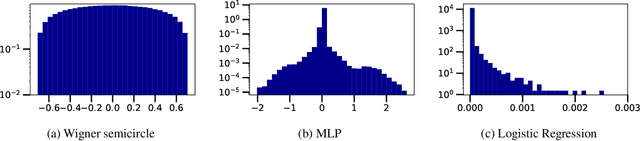
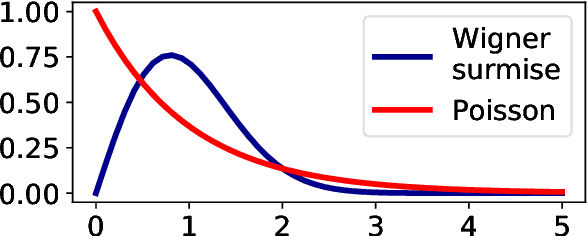
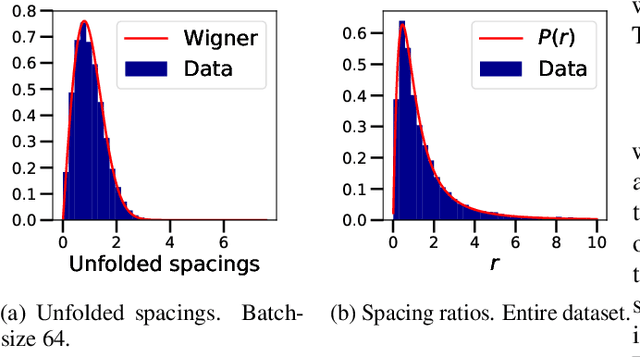
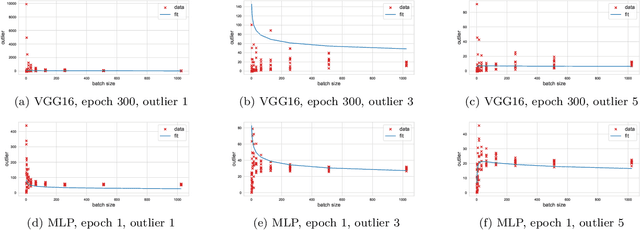
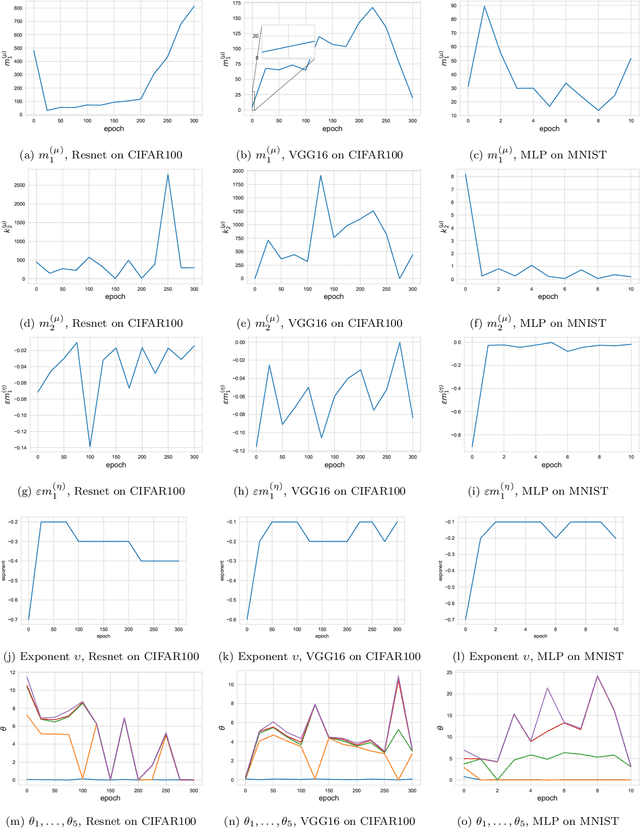
We investigate the local spectral statistics of the loss surface Hessians of artificial neural networks, where we discover excellent agreement with Gaussian Orthogonal Ensemble statistics across several network architectures and datasets. These results shed new light on the applicability of Random Matrix Theory to modelling neural networks and suggest a previously unrecognised role for it in the study of loss surfaces in deep learning. Inspired by these observations, we propose a novel model for the true loss surfaces of neural networks, consistent with our observations, which allows for Hessian spectral densities with rank degeneracy and outliers, extensively observed in practice, and predicts a growing independence of loss gradients as a function of distance in weight-space. We further investigate the importance of the true loss surface in neural networks and find, in contrast to previous work, that the exponential hardness of locating the global minimum has practical consequences for achieving state of the art performance.

A spin-glass model for the loss surfaces of generative adversarial networks

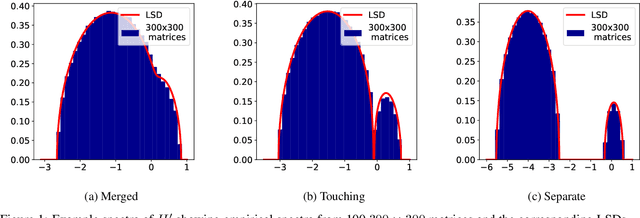
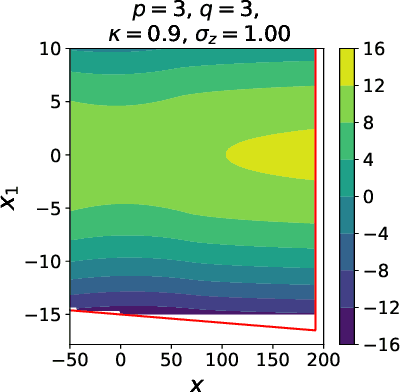
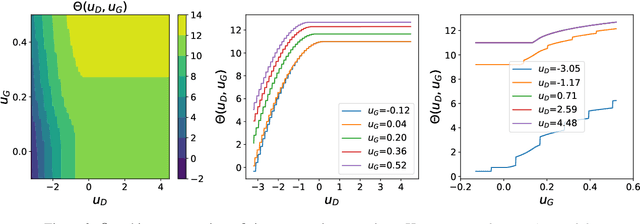
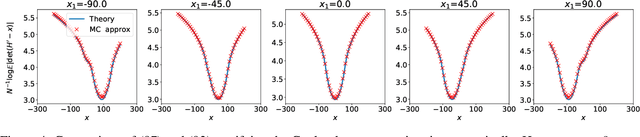
We present a novel mathematical model that seeks to capture the key design feature of generative adversarial networks (GANs). Our model consists of two interacting spin glasses, and we conduct an extensive theoretical analysis of the complexity of the model's critical points using techniques from Random Matrix Theory. The result is insights into the loss surfaces of large GANs that build upon prior insights for simpler networks, but also reveal new structure unique to this setting.