Francesco Mezzadri
Universal characteristics of deep neural network loss surfaces from random matrix theory
May 17, 2022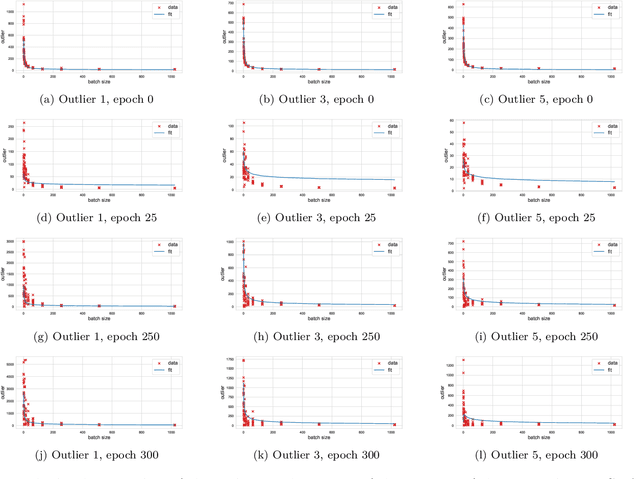
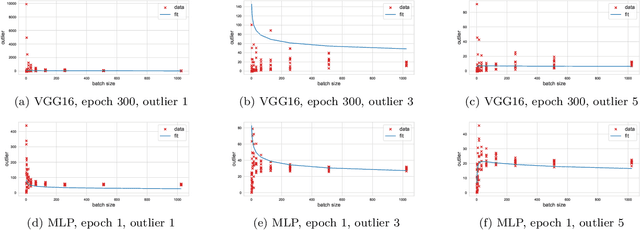
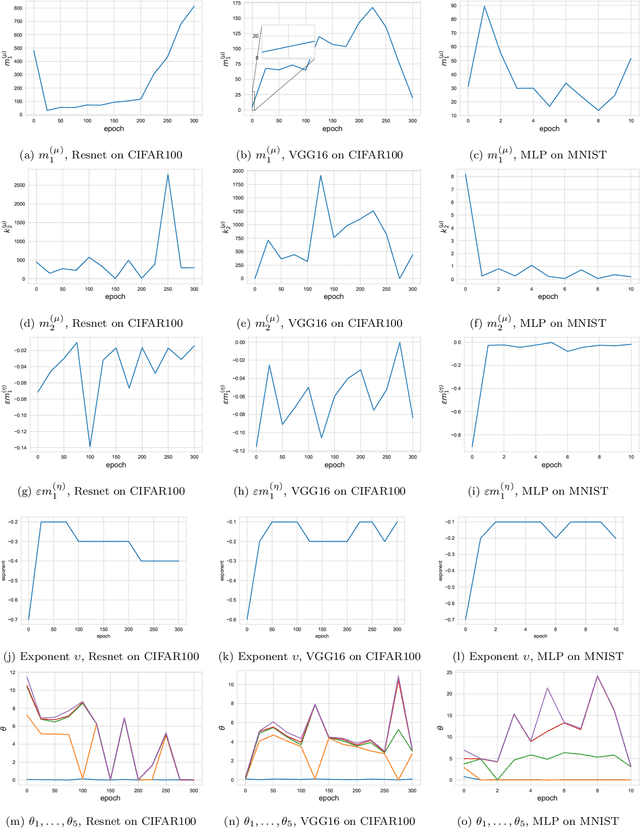
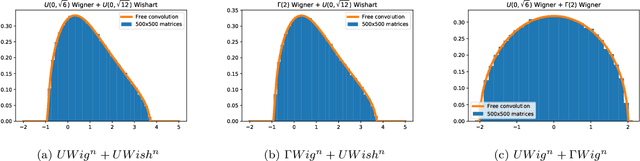
Abstract:This paper considers several aspects of random matrix universality in deep neural networks. Motivated by recent experimental work, we use universal properties of random matrices related to local statistics to derive practical implications for deep neural networks based on a realistic model of their Hessians. In particular we derive universal aspects of outliers in the spectra of deep neural networks and demonstrate the important role of random matrix local laws in popular pre-conditioning gradient descent algorithms. We also present insights into deep neural network loss surfaces from quite general arguments based on tools from statistical physics and random matrix theory.
A spin-glass model for the loss surfaces of generative adversarial networks
Jan 07, 2021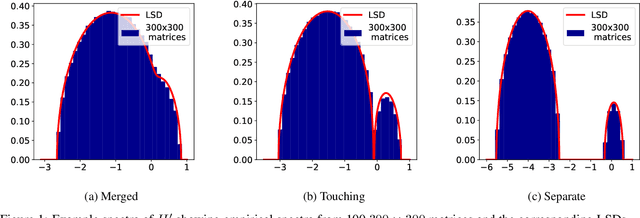
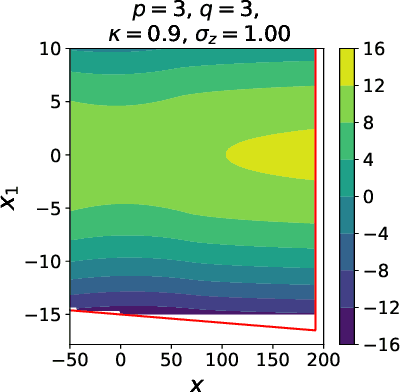
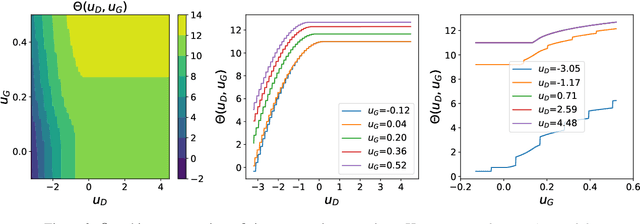
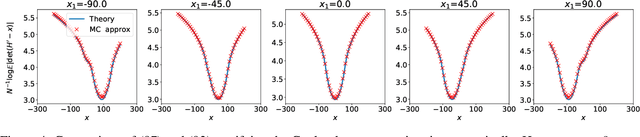
Abstract:We present a novel mathematical model that seeks to capture the key design feature of generative adversarial networks (GANs). Our model consists of two interacting spin glasses, and we conduct an extensive theoretical analysis of the complexity of the model's critical points using techniques from Random Matrix Theory. The result is insights into the loss surfaces of large GANs that build upon prior insights for simpler networks, but also reveal new structure unique to this setting.
The Loss Surfaces of Neural Networks with General Activation Functions
Apr 16, 2020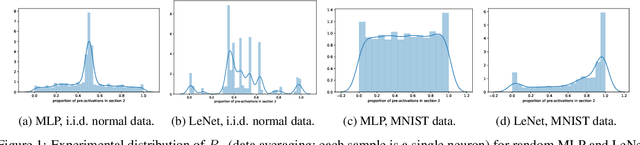

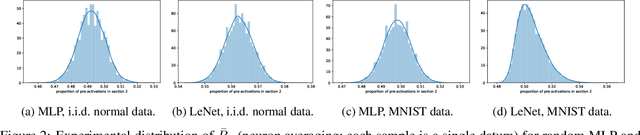

Abstract:We present results extending the foundational work of Choromanska et al (2015) on the complexity of the loss surfaces of multi-layer neural networks. We remove the strict reliance on specifically ReLU activation functions and obtain broadly the same results for general activation functions. This is achieved with piece-wise linear approximations to general activation functions, Kac-Rice calculations akin to those of Auffinger, Ben Arous and \v{C}ern\`y (2013), Fyodorov (2004), Fyodorov and Williams (2007) and asymptotic analysis made possible by supersymmetric methods. Our results strengthen the case for the conclusions of Choromanska et al (2015) and the calculations contain various novel details required to deal with certain perturbations to the classical spin-glass calculations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge