The Implicit Bias of Depth: From Neural Collapse to Softmax Codes

Neural collapse (NC) describes the structured geometry that emerges in the features and weights of trained classifiers. Recent theory suggests NC can be suboptimal in deep architectures, attributing this to an explicit low-rank bias from L2 regularization. We study the deep unconstrained feature model (UFM)-equivalent to a deep linear network with orthogonal inputs-trained without regularization, to isolate how gradient descent and depth alone shape NC. We show that depth induces an implicit low-rank bias: low-rank matrices propagate norm more efficiently through successive multiplications, promoting low-rank alternatives to NC. These alternatives, we argue, correspond to softmax codes: max-margin solutions previously found in width-bottlenecked networks. Analyzing training dynamics under spectral initialization, we identify an early-time repulsion among singular values that drives low-rank emergence, and characterize how depth shrinks NC's basin of attraction. Finally, we show that some effects act in the opposite direction: for randomly initialized networks, increasing width biases training toward higher-rank solutions. Our results provide the first asymptotic and dynamic characterization of implicit bias in deep UFMs trained with unregularized multiclass cross-entropy.

When Stronger Triggers Backfire: A High-Dimensional Theory of Backdoor Attacks

Backdoor poisoning attacks behave counter-intuitively in high dimensions: stronger training triggers can help the defender. We study regularised generalised linear models on Gaussian-mixture data in the proportional regime ($p/n \to κ$), varying the training trigger strength $α$ against a fixed test trigger. Three phenomena emerge: (i) clean test accuracy increases with $α$; (ii) attack success peaks at a finite $α$ and then declines; and (iii) the most damaging trigger direction is the minimum eigenvector of the data covariance. We prove all three results in closed form for the squared loss, and extend (i) and (ii) to general convex GLM losses via a Gaussian-proxy fixed-point system. We identify a finite-sample noise floor proportional to $κ$ as the mechanism behind (i), invisible to classical $n \gg p$ analysis. Experiments on CIFAR-10 and Gaussian surrogates match the theory closely; ResNet-18 experiments show the same phenomena beyond the convex setting.

The Persistence of Neural Collapse Despite Low-Rank Bias: An Analytic Perspective Through Unconstrained Features

Modern deep neural networks have been observed to exhibit a simple structure in their final layer features and weights, commonly referred to as neural collapse. This phenomenon has also been noted in layers beyond the final one, an extension known as deep neural collapse. Recent findings indicate that such a structure is generally not optimal in the deep unconstrained feature model, an approximation of an expressive network. This is attributed to a low-rank bias induced by regularization, which favors solutions with lower-rank than those typically associated with deep neural collapse. In this work, we extend these observations to the cross-entropy loss and analyze how the low-rank bias influences various solutions. Additionally, we explore how this bias induces specific structures in the singular values of the weights at global optima. Furthermore, we examine the loss surface of these models and provide evidence that the frequent observation of deep neural collapse in practice, despite its suboptimality, may result from its higher degeneracy on the loss surface.

Unifying Low Dimensional Observations in Deep Learning Through the Deep Linear Unconstrained Feature Model

Modern deep neural networks have achieved high performance across various tasks. Recently, researchers have noted occurrences of low-dimensional structure in the weights, Hessian's, gradients, and feature vectors of these networks, spanning different datasets and architectures when trained to convergence. In this analysis, we theoretically demonstrate these observations arising, and show how they can be unified within a generalized unconstrained feature model that can be considered analytically. Specifically, we consider a previously described structure called Neural Collapse, and its multi-layer counterpart, Deep Neural Collapse, which emerges when the network approaches global optima. This phenomenon explains the other observed low-dimensional behaviours on a layer-wise level, such as the bulk and outlier structure seen in Hessian spectra, and the alignment of gradient descent with the outlier eigenspace of the Hessian. Empirical results in both the deep linear unconstrained feature model and its non-linear equivalent support these predicted observations.

The Loss Surfaces of Neural Networks with General Activation Functions

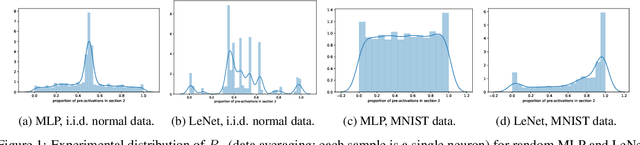
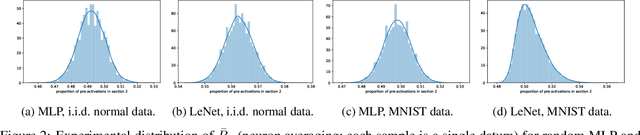
We present results extending the foundational work of Choromanska et al (2015) on the complexity of the loss surfaces of multi-layer neural networks. We remove the strict reliance on specifically ReLU activation functions and obtain broadly the same results for general activation functions. This is achieved with piece-wise linear approximations to general activation functions, Kac-Rice calculations akin to those of Auffinger, Ben Arous and \v{C}ern\`y (2013), Fyodorov (2004), Fyodorov and Williams (2007) and asymptotic analysis made possible by supersymmetric methods. Our results strengthen the case for the conclusions of Choromanska et al (2015) and the calculations contain various novel details required to deal with certain perturbations to the classical spin-glass calculations.