The Loss Surfaces of Neural Networks with General Activation Functions
Paper and Code
Apr 16, 2020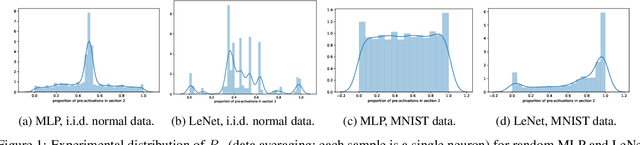

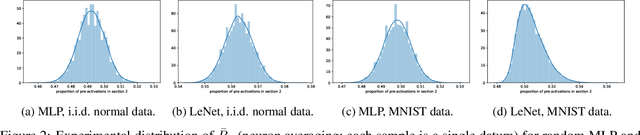

We present results extending the foundational work of Choromanska et al (2015) on the complexity of the loss surfaces of multi-layer neural networks. We remove the strict reliance on specifically ReLU activation functions and obtain broadly the same results for general activation functions. This is achieved with piece-wise linear approximations to general activation functions, Kac-Rice calculations akin to those of Auffinger, Ben Arous and \v{C}ern\`y (2013), Fyodorov (2004), Fyodorov and Williams (2007) and asymptotic analysis made possible by supersymmetric methods. Our results strengthen the case for the conclusions of Choromanska et al (2015) and the calculations contain various novel details required to deal with certain perturbations to the classical spin-glass calculations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge