Thomas Frerix
Variational Data Assimilation with a Learned Inverse Observation Operator
Feb 22, 2021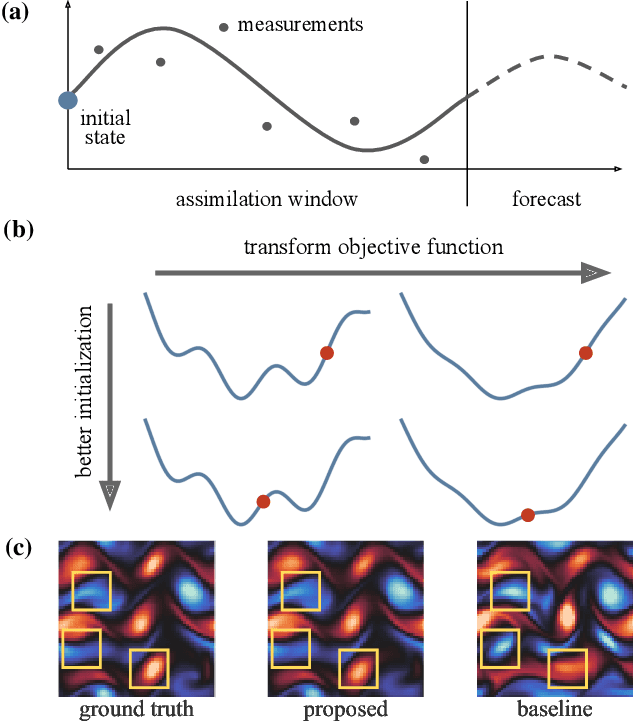
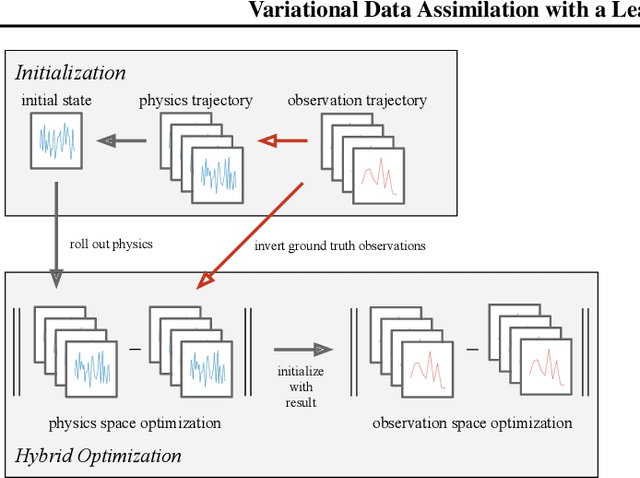

Abstract:Variational data assimilation optimizes for an initial state of a dynamical system such that its evolution fits observational data. The physical model can subsequently be evolved into the future to make predictions. This principle is a cornerstone of large scale forecasting applications such as numerical weather prediction. As such, it is implemented in current operational systems of weather forecasting agencies across the globe. However, finding a good initial state poses a difficult optimization problem in part due to the non-invertible relationship between physical states and their corresponding observations. We learn a mapping from observational data to physical states and show how it can be used to improve optimizability. We employ this mapping in two ways: to better initialize the non-convex optimization problem, and to reformulate the objective function in better behaved physics space instead of observation space. Our experimental results for the Lorenz96 model and a two-dimensional turbulent fluid flow demonstrate that this procedure significantly improves forecast quality for chaotic systems.
Linear Inequality Constraints for Neural Network Activations
Feb 06, 2019

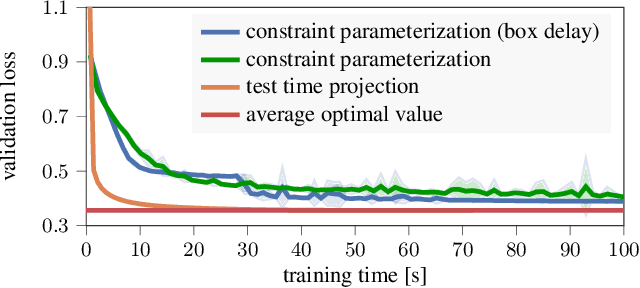
Abstract:We propose a method to impose linear inequality constraints on neural network activations. The proposed method allows a data-driven training approach to be combined with modeling prior knowledge about the task. Our algorithm computes a suitable parameterization of the feasible set at initialization and uses standard variants of stochastic gradient descent to find solutions to the constrained network. Thus, the modeling constraints are always satisfied during training. Crucially, our approach avoids to solve a sub-optimization problem at each training step or to manually trade-off data and constraint fidelity with additional hyperparameters. We consider constrained generative modeling as an important application domain and experimentally demonstrate the proposed method by constraining a variational autoencoder.
Proximal Backpropagation
Feb 20, 2018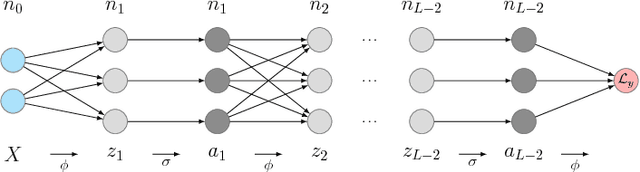
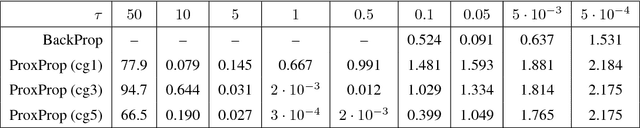
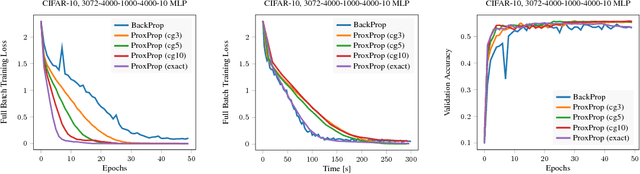
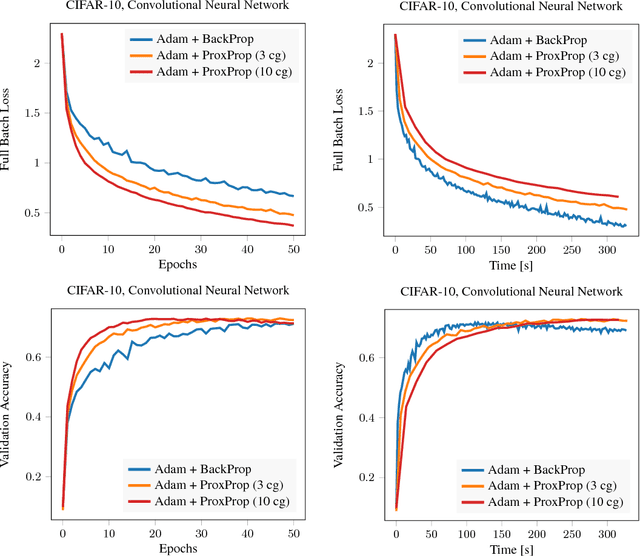
Abstract:We propose proximal backpropagation (ProxProp) as a novel algorithm that takes implicit instead of explicit gradient steps to update the network parameters during neural network training. Our algorithm is motivated by the step size limitation of explicit gradient descent, which poses an impediment for optimization. ProxProp is developed from a general point of view on the backpropagation algorithm, currently the most common technique to train neural networks via stochastic gradient descent and variants thereof. Specifically, we show that backpropagation of a prediction error is equivalent to sequential gradient descent steps on a quadratic penalty energy, which comprises the network activations as variables of the optimization. We further analyze theoretical properties of ProxProp and in particular prove that the algorithm yields a descent direction in parameter space and can therefore be combined with a wide variety of convergent algorithms. Finally, we devise an efficient numerical implementation that integrates well with popular deep learning frameworks. We conclude by demonstrating promising numerical results and show that ProxProp can be effectively combined with common first order optimizers such as Adam.
Associative Domain Adaptation
Aug 02, 2017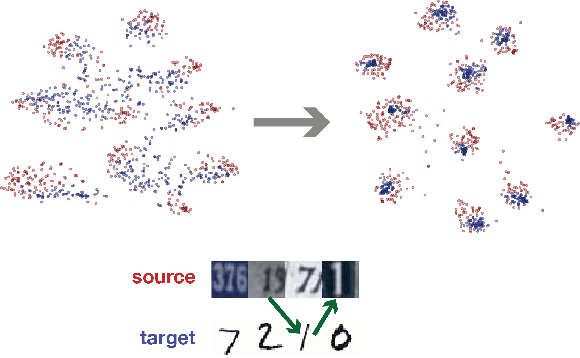



Abstract:We propose associative domain adaptation, a novel technique for end-to-end domain adaptation with neural networks, the task of inferring class labels for an unlabeled target domain based on the statistical properties of a labeled source domain. Our training scheme follows the paradigm that in order to effectively derive class labels for the target domain, a network should produce statistically domain invariant embeddings, while minimizing the classification error on the labeled source domain. We accomplish this by reinforcing associations between source and target data directly in embedding space. Our method can easily be added to any existing classification network with no structural and almost no computational overhead. We demonstrate the effectiveness of our approach on various benchmarks and achieve state-of-the-art results across the board with a generic convolutional neural network architecture not specifically tuned to the respective tasks. Finally, we show that the proposed association loss produces embeddings that are more effective for domain adaptation compared to methods employing maximum mean discrepancy as a similarity measure in embedding space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge