Proximal Backpropagation
Paper and Code
Feb 20, 2018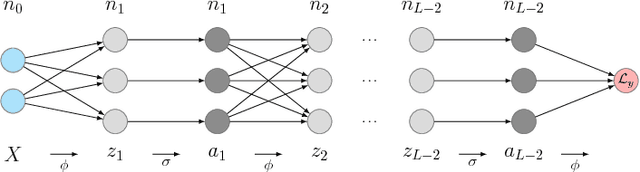
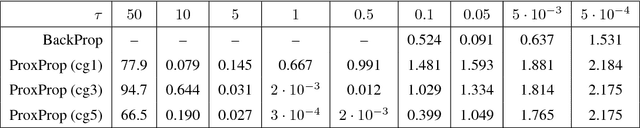
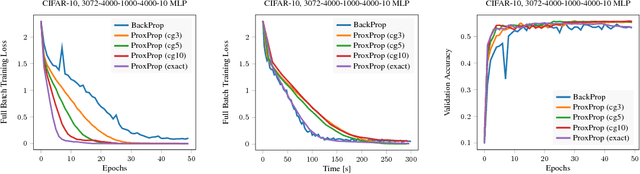
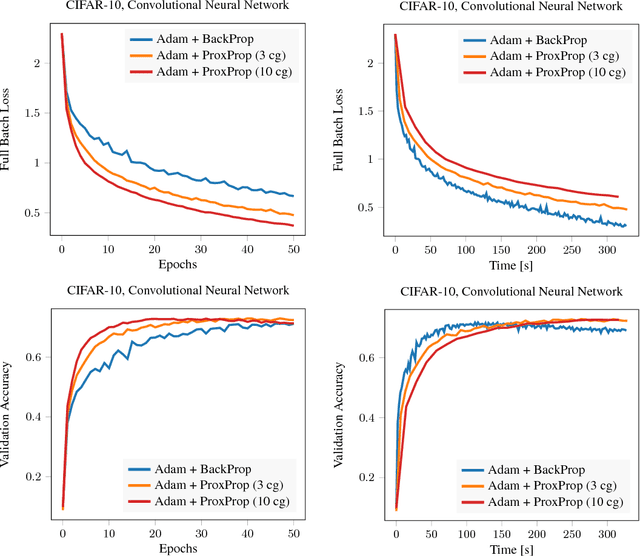
We propose proximal backpropagation (ProxProp) as a novel algorithm that takes implicit instead of explicit gradient steps to update the network parameters during neural network training. Our algorithm is motivated by the step size limitation of explicit gradient descent, which poses an impediment for optimization. ProxProp is developed from a general point of view on the backpropagation algorithm, currently the most common technique to train neural networks via stochastic gradient descent and variants thereof. Specifically, we show that backpropagation of a prediction error is equivalent to sequential gradient descent steps on a quadratic penalty energy, which comprises the network activations as variables of the optimization. We further analyze theoretical properties of ProxProp and in particular prove that the algorithm yields a descent direction in parameter space and can therefore be combined with a wide variety of convergent algorithms. Finally, we devise an efficient numerical implementation that integrates well with popular deep learning frameworks. We conclude by demonstrating promising numerical results and show that ProxProp can be effectively combined with common first order optimizers such as Adam.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge