Computational Life: How Well-formed, Self-replicating Programs Emerge from Simple Interaction

The fields of Origin of Life and Artificial Life both question what life is and how it emerges from a distinct set of "pre-life" dynamics. One common feature of most substrates where life emerges is a marked shift in dynamics when self-replication appears. While there are some hypotheses regarding how self-replicators arose in nature, we know very little about the general dynamics, computational principles, and necessary conditions for self-replicators to emerge. This is especially true on "computational substrates" where interactions involve logical, mathematical, or programming rules. In this paper we take a step towards understanding how self-replicators arise by studying several computational substrates based on various simple programming languages and machine instruction sets. We show that when random, non self-replicating programs are placed in an environment lacking any explicit fitness landscape, self-replicators tend to arise. We demonstrate how this occurs due to random interactions and self-modification, and can happen with and without background random mutations. We also show how increasingly complex dynamics continue to emerge following the rise of self-replicators. Finally, we show a counterexample of a minimalistic programming language where self-replicators are possible, but so far have not been observed to arise.

Mesh Neural Cellular Automata

Modeling and synthesizing textures are essential for enhancing the realism of virtual environments. Methods that directly synthesize textures in 3D offer distinct advantages to the UV-mapping-based methods as they can create seamless textures and align more closely with the ways textures form in nature. We propose Mesh Neural Cellular Automata (MeshNCA), a method for directly synthesizing dynamic textures on 3D meshes without requiring any UV maps. MeshNCA is a generalized type of cellular automata that can operate on a set of cells arranged on a non-grid structure such as vertices of a 3D mesh. While only being trained on an Icosphere mesh, MeshNCA shows remarkable generalization and can synthesize textures on any mesh in real time after the training. Additionally, it accommodates multi-modal supervision and can be trained using different targets such as images, text prompts, and motion vector fields. Moreover, we conceptualize a way of grafting trained MeshNCA instances, enabling texture interpolation. Our MeshNCA model enables real-time 3D texture synthesis on meshes and allows several user interactions including texture density/orientation control, a grafting brush, and motion speed/direction control. Finally, we implement the forward pass of our MeshNCA model using the WebGL shading language and showcase our trained models in an online interactive demo which is accessible on personal computers and smartphones. Our demo and the high resolution version of this PDF are available at https://meshnca.github.io/.

Biomaker CA: a Biome Maker project using Cellular Automata

We introduce Biomaker CA: a Biome Maker project using Cellular Automata (CA). In Biomaker CA, morphogenesis is a first class citizen and small seeds need to grow into plant-like organisms to survive in a nutrient starved environment and eventually reproduce with variation so that a biome survives for long timelines. We simulate complex biomes by means of CA rules in 2D grids and parallelize all of its computation on GPUs through the Python JAX framework. We show how this project allows for several different kinds of environments and laws of 'physics', alongside different model architectures and mutation strategies. We further analyze some configurations to show how plant agents can grow, survive, reproduce, and evolve, forming stable and unstable biomes. We then demonstrate how one can meta-evolve models to survive in a harsh environment either through end-to-end meta-evolution or by a more surgical and efficient approach, called Petri dish meta-evolution. Finally, we show how to perform interactive evolution, where the user decides how to evolve a plant model interactively and then deploys it in a larger environment. We open source Biomaker CA at: https://tinyurl.com/2x8yu34s .

Growing Steerable Neural Cellular Automata

Neural Cellular Automata (NCA) models have shown remarkable capacity for pattern formation and complex global behaviors stemming from local coordination. However, in the original implementation of NCA, cells are incapable of adjusting their own orientation, and it is the responsibility of the model designer to orient them externally. A recent isotropic variant of NCA (Growing Isotropic Neural Cellular Automata) makes the model orientation-independent - cells can no longer tell up from down, nor left from right - by removing its dependency on perceiving the gradient of spatial states in its neighborhood. In this work, we revisit NCA with a different approach: we make each cell responsible for its own orientation by allowing it to "turn" as determined by an adjustable internal state. The resulting Steerable NCA contains cells of varying orientation embedded in the same pattern. We observe how, while Isotropic NCA are orientation-agnostic, Steerable NCA have chirality: they have a predetermined left-right symmetry. We therefore show that we can train Steerable NCA in similar but simpler ways than their Isotropic variant by: (1) breaking symmetries using only two seeds, or (2) introducing a rotation-invariant training objective and relying on asynchronous cell updates to break the up-down symmetry of the system.

Differentiable Programming of Chemical Reaction Networks

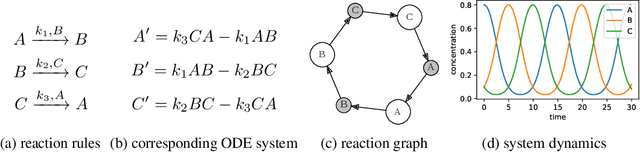
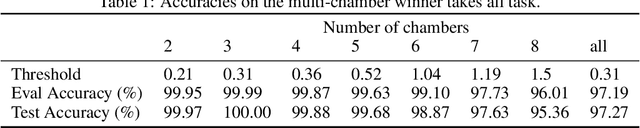
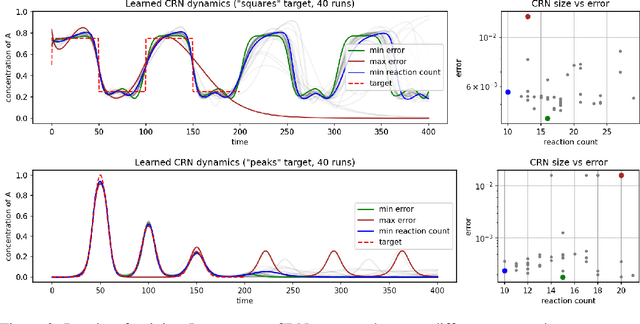
We present a differentiable formulation of abstract chemical reaction networks (CRNs) that can be trained to solve a variety of computational tasks. Chemical reaction networks are one of the most fundamental computational substrates used by nature. We study well-mixed single-chamber systems, as well as systems with multiple chambers separated by membranes, under mass-action kinetics. We demonstrate that differentiable optimisation, combined with proper regularisation, can discover non-trivial sparse reaction networks that can implement various sorts of oscillators and other chemical computing devices.

Transformers learn in-context by gradient descent

Transformers have become the state-of-the-art neural network architecture across numerous domains of machine learning. This is partly due to their celebrated ability to transfer and to learn in-context based on few examples. Nevertheless, the mechanisms by which Transformers become in-context learners are not well understood and remain mostly an intuition. Here, we argue that training Transformers on auto-regressive tasks can be closely related to well-known gradient-based meta-learning formulations. We start by providing a simple weight construction that shows the equivalence of data transformations induced by 1) a single linear self-attention layer and by 2) gradient-descent (GD) on a regression loss. Motivated by that construction, we show empirically that when training self-attention-only Transformers on simple regression tasks either the models learned by GD and Transformers show great similarity or, remarkably, the weights found by optimization match the construction. Thus we show how trained Transformers implement gradient descent in their forward pass. This allows us, at least in the domain of regression problems, to mechanistically understand the inner workings of optimized Transformers that learn in-context. Furthermore, we identify how Transformers surpass plain gradient descent by an iterative curvature correction and learn linear models on deep data representations to solve non-linear regression tasks. Finally, we discuss intriguing parallels to a mechanism identified to be crucial for in-context learning termed induction-head (Olsson et al., 2022) and show how it could be understood as a specific case of in-context learning by gradient descent learning within Transformers.

Growing Isotropic Neural Cellular Automata

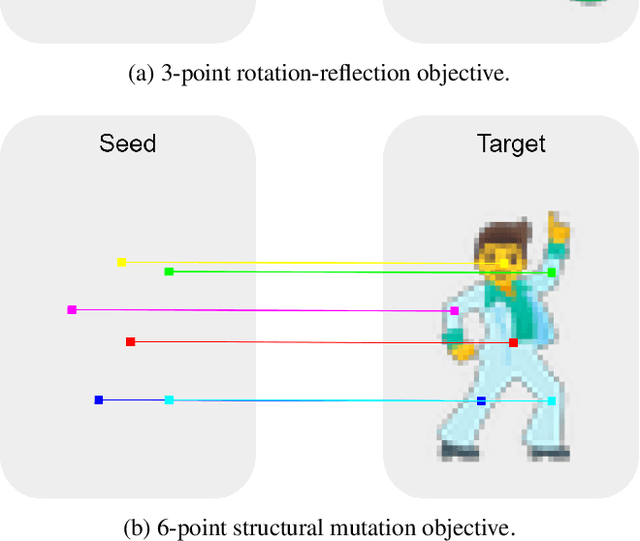
Modeling the ability of multicellular organisms to build and maintain their bodies through local interactions between individual cells (morphogenesis) is a long-standing challenge of developmental biology. Recently, the Neural Cellular Automata (NCA) model was proposed as a way to find local system rules that produce a desired global behaviour, such as growing and persisting a predefined pattern, by repeatedly applying the same rule over a grid starting from a single cell. In this work we argue that the original Growing NCA model has an important limitation: anisotropy of the learned update rule. This implies the presence of an external factor that orients the cells in a particular direction. In other words, 'physical' rules of the underlying system are not invariant to rotation, thus prohibiting the existence of differently oriented instances of the target pattern on the same grid. We propose a modified Isotropic NCA model that does not have this limitation. We demonstrate that cell systems can be trained to grow accurate asymmetrical patterns through either of two methods: by breaking symmetries using structured seeds; or by introducing a rotation-reflection invariant training objective and relying on symmetry breaking caused by asynchronous cell updates.

$μ$NCA: Texture Generation with Ultra-Compact Neural Cellular Automata

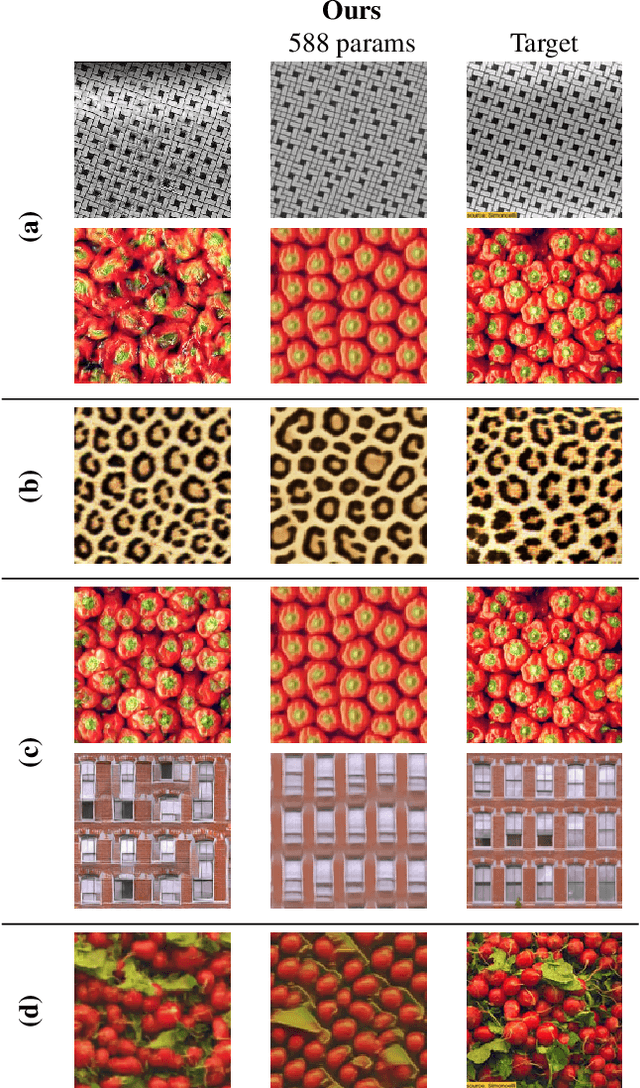
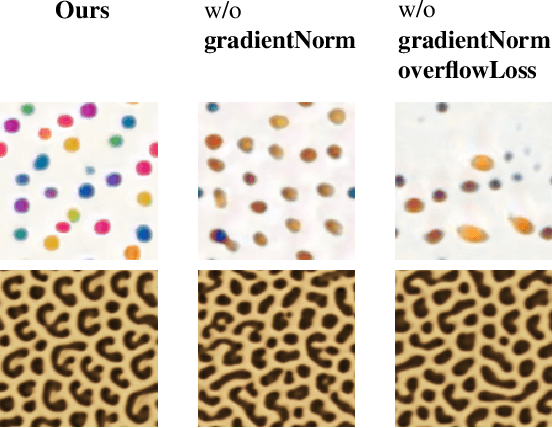
We study the problem of example-based procedural texture synthesis using highly compact models. Given a sample image, we use differentiable programming to train a generative process, parameterised by a recurrent Neural Cellular Automata (NCA) rule. Contrary to the common belief that neural networks should be significantly over-parameterised, we demonstrate that our model architecture and training procedure allows for representing complex texture patterns using just a few hundred learned parameters, making their expressivity comparable to hand-engineered procedural texture generating programs. The smallest models from the proposed $\mu$NCA family scale down to 68 parameters. When using quantisation to one byte per parameter, proposed models can be shrunk to a size range between 588 and 68 bytes. Implementation of a texture generator that uses these parameters to produce images is possible with just a few lines of GLSL or C code.

Differentiable Programming of Reaction-Diffusion Patterns

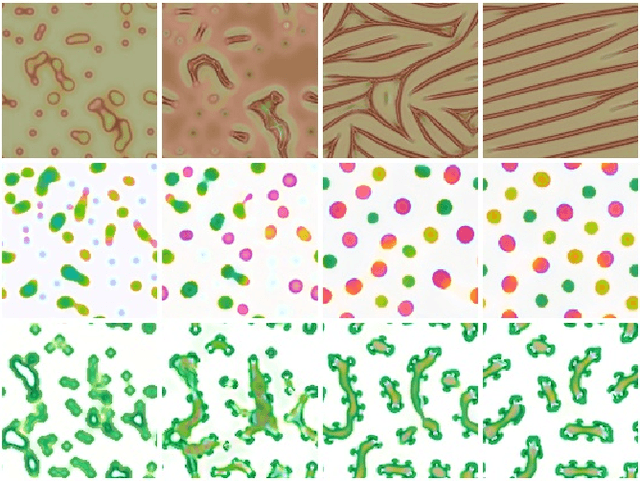
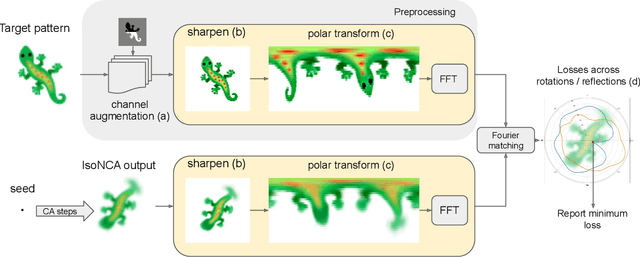
Reaction-Diffusion (RD) systems provide a computational framework that governs many pattern formation processes in nature. Current RD system design practices boil down to trial-and-error parameter search. We propose a differentiable optimization method for learning the RD system parameters to perform example-based texture synthesis on a 2D plane. We do this by representing the RD system as a variant of Neural Cellular Automata and using task-specific differentiable loss functions. RD systems generated by our method exhibit robust, non-trivial 'life-like' behavior.

Texture Generation with Neural Cellular Automata

Neural Cellular Automata (NCA) have shown a remarkable ability to learn the required rules to "grow" images, classify morphologies, segment images, as well as to do general computation such as path-finding. We believe the inductive prior they introduce lends itself to the generation of textures. Textures in the natural world are often generated by variants of locally interacting reaction-diffusion systems. Human-made textures are likewise often generated in a local manner (textile weaving, for instance) or using rules with local dependencies (regular grids or geometric patterns). We demonstrate learning a texture generator from a single template image, with the generation method being embarrassingly parallel, exhibiting quick convergence and high fidelity of output, and requiring only some minimal assumptions around the underlying state manifold. Furthermore, we investigate properties of the learned models that are both useful and interesting, such as non-stationary dynamics and an inherent robustness to damage. Finally, we make qualitative claims that the behaviour exhibited by the NCA model is a learned, distributed, local algorithm to generate a texture, setting our method apart from existing work on texture generation. We discuss the advantages of such a paradigm.