Growing Steerable Neural Cellular Automata

Neural Cellular Automata (NCA) models have shown remarkable capacity for pattern formation and complex global behaviors stemming from local coordination. However, in the original implementation of NCA, cells are incapable of adjusting their own orientation, and it is the responsibility of the model designer to orient them externally. A recent isotropic variant of NCA (Growing Isotropic Neural Cellular Automata) makes the model orientation-independent - cells can no longer tell up from down, nor left from right - by removing its dependency on perceiving the gradient of spatial states in its neighborhood. In this work, we revisit NCA with a different approach: we make each cell responsible for its own orientation by allowing it to "turn" as determined by an adjustable internal state. The resulting Steerable NCA contains cells of varying orientation embedded in the same pattern. We observe how, while Isotropic NCA are orientation-agnostic, Steerable NCA have chirality: they have a predetermined left-right symmetry. We therefore show that we can train Steerable NCA in similar but simpler ways than their Isotropic variant by: (1) breaking symmetries using only two seeds, or (2) introducing a rotation-invariant training objective and relying on asynchronous cell updates to break the up-down symmetry of the system.

Growing Isotropic Neural Cellular Automata

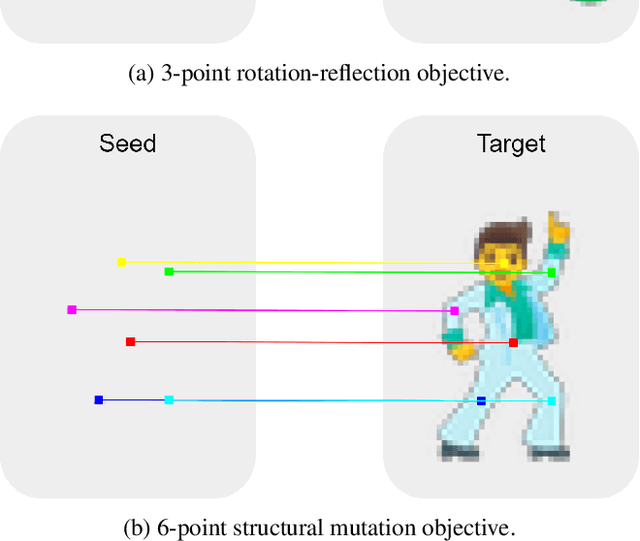
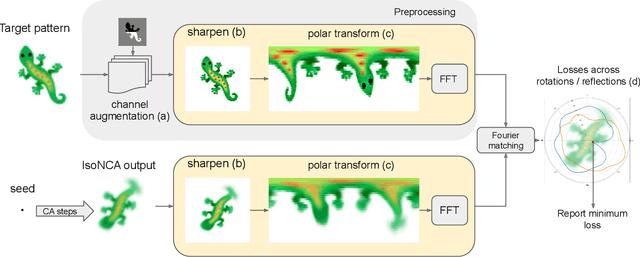
Modeling the ability of multicellular organisms to build and maintain their bodies through local interactions between individual cells (morphogenesis) is a long-standing challenge of developmental biology. Recently, the Neural Cellular Automata (NCA) model was proposed as a way to find local system rules that produce a desired global behaviour, such as growing and persisting a predefined pattern, by repeatedly applying the same rule over a grid starting from a single cell. In this work we argue that the original Growing NCA model has an important limitation: anisotropy of the learned update rule. This implies the presence of an external factor that orients the cells in a particular direction. In other words, 'physical' rules of the underlying system are not invariant to rotation, thus prohibiting the existence of differently oriented instances of the target pattern on the same grid. We propose a modified Isotropic NCA model that does not have this limitation. We demonstrate that cell systems can be trained to grow accurate asymmetrical patterns through either of two methods: by breaking symmetries using structured seeds; or by introducing a rotation-reflection invariant training objective and relying on symmetry breaking caused by asynchronous cell updates.