Growing Isotropic Neural Cellular Automata
Paper and Code
May 03, 2022
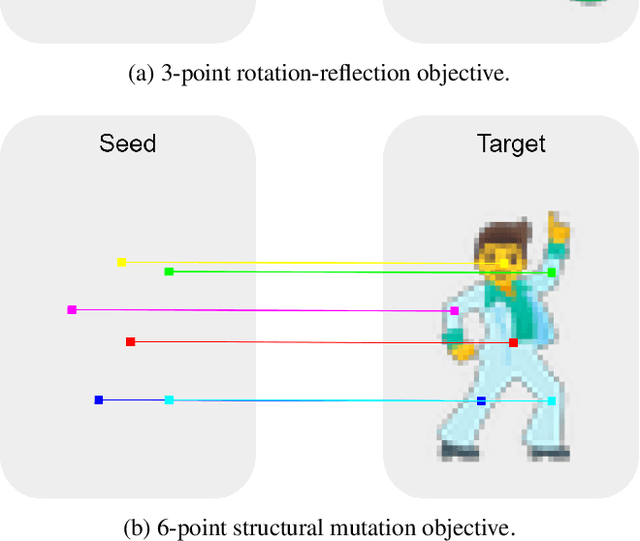
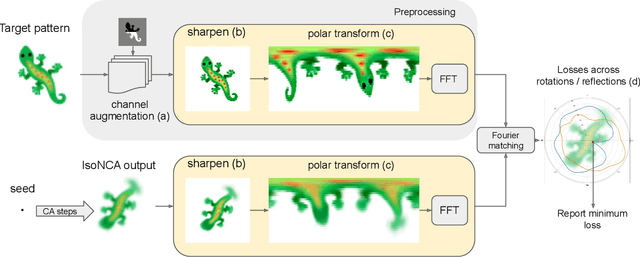

Modeling the ability of multicellular organisms to build and maintain their bodies through local interactions between individual cells (morphogenesis) is a long-standing challenge of developmental biology. Recently, the Neural Cellular Automata (NCA) model was proposed as a way to find local system rules that produce a desired global behaviour, such as growing and persisting a predefined pattern, by repeatedly applying the same rule over a grid starting from a single cell. In this work we argue that the original Growing NCA model has an important limitation: anisotropy of the learned update rule. This implies the presence of an external factor that orients the cells in a particular direction. In other words, 'physical' rules of the underlying system are not invariant to rotation, thus prohibiting the existence of differently oriented instances of the target pattern on the same grid. We propose a modified Isotropic NCA model that does not have this limitation. We demonstrate that cell systems can be trained to grow accurate asymmetrical patterns through either of two methods: by breaking symmetries using structured seeds; or by introducing a rotation-reflection invariant training objective and relying on symmetry breaking caused by asynchronous cell updates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge