Guided Diffusion Sampling on Function Spaces with Applications to PDEs

We propose a general framework for conditional sampling in PDE-based inverse problems, targeting the recovery of whole solutions from extremely sparse or noisy measurements. This is accomplished by a function-space diffusion model and plug-and-play guidance for conditioning. Our method first trains an unconditional discretization-agnostic denoising model using neural operator architectures. At inference, we refine the samples to satisfy sparse observation data via a gradient-based guidance mechanism. Through rigorous mathematical analysis, we extend Tweedie's formula to infinite-dimensional Hilbert spaces, providing the theoretical foundation for our posterior sampling approach. Our method (FunDPS) accurately captures posterior distributions in function spaces under minimal supervision and severe data scarcity. Across five PDE tasks with only 3% observation, our method achieves an average 32% accuracy improvement over state-of-the-art fixed-resolution diffusion baselines while reducing sampling steps by 4x. Furthermore, multi-resolution fine-tuning ensures strong cross-resolution generalizability. To the best of our knowledge, this is the first diffusion-based framework to operate independently of discretization, offering a practical and flexible solution for forward and inverse problems in the context of PDEs. Code is available at https://github.com/neuraloperator/FunDPS

EventFlow: Forecasting Continuous-Time Event Data with Flow Matching

Continuous-time event sequences, in which events occur at irregular intervals, are ubiquitous across a wide range of industrial and scientific domains. The contemporary modeling paradigm is to treat such data as realizations of a temporal point process, and in machine learning it is common to model temporal point processes in an autoregressive fashion using a neural network. While autoregressive models are successful in predicting the time of a single subsequent event, their performance can be unsatisfactory in forecasting longer horizons due to cascading errors. We propose EventFlow, a non-autoregressive generative model for temporal point processes. Our model builds on the flow matching framework in order to directly learn joint distributions over event times, side-stepping the autoregressive process. EventFlow is likelihood-free, easy to implement and sample from, and either matches or surpasses the performance of state-of-the-art models in both unconditional and conditional generation tasks on a set of standard benchmarks

Dynamic Conditional Optimal Transport through Simulation-Free Flows

We study the geometry of conditional optimal transport (COT) and prove a dynamical formulation which generalizes the Benamou-Brenier Theorem. With these tools, we propose a simulation-free flow-based method for conditional generative modeling. Our method couples an arbitrary source distribution to a specified target distribution through a triangular COT plan. We build on the framework of flow matching to train a conditional generative model by approximating the geodesic path of measures induced by this COT plan. Our theory and methods are applicable in the infinite-dimensional setting, making them well suited for inverse problems. Empirically, we demonstrate our proposed method on two image-to-image translation tasks and an infinite-dimensional Bayesian inverse problem.

Probabilistic Precipitation Downscaling with Optical Flow-Guided Diffusion

In climate science and meteorology, local precipitation predictions are limited by the immense computational costs induced by the high spatial resolution that simulation methods require. A common workaround is statistical downscaling (aka superresolution), where a low-resolution prediction is super-resolved using statistical approaches. While traditional computer vision tasks mainly focus on human perception or mean squared error, applications in weather and climate require capturing the conditional distribution of high-resolution patterns given low-resolution patterns so that reliable ensemble averages can be taken. Our approach relies on extending recent video diffusion models to precipitation superresolution: an optical flow on the high-resolution output induces temporally coherent predictions, whereas a temporally-conditioned diffusion model generates residuals that capture the correct noise characteristics and high-frequency patterns. We test our approach on X-SHiELD, an established large-scale climate simulation dataset, and compare against two state-of-the-art baselines, focusing on CRPS, MSE, precipitation distributions, as well as an illustrative case -- the complex terrain of California. Our approach sets a new standard for data-driven precipitation downscaling.

Functional Flow Matching

In this work, we propose Functional Flow Matching (FFM), a function-space generative model that generalizes the recently-introduced Flow Matching model to operate directly in infinite-dimensional spaces. Our approach works by first defining a path of probability measures that interpolates between a fixed Gaussian measure and the data distribution, followed by learning a vector field on the underlying space of functions that generates this path of measures. Our method does not rely on likelihoods or simulations, making it well-suited to the function space setting. We provide both a theoretical framework for building such models and an empirical evaluation of our techniques. We demonstrate through experiments on synthetic and real-world benchmarks that our proposed FFM method outperforms several recently proposed function-space generative models.

Diffusion Generative Models in Infinite Dimensions

Diffusion generative models have recently been applied to domains where the available data can be seen as a discretization of an underlying function, such as audio signals or time series. However, these models operate directly on the discretized data, and there are no semantics in the modeling process that relate the observed data to the underlying functional forms. We generalize diffusion models to operate directly in function space by developing the foundational theory for such models in terms of Gaussian measures on Hilbert spaces. A significant benefit of our function space point of view is that it allows us to explicitly specify the space of functions we are working in, leading us to develop methods for diffusion generative modeling in Sobolev spaces. Our approach allows us to perform both unconditional and conditional generation of function-valued data. We demonstrate our methods on several synthetic and real-world benchmarks.

Combining Human Predictions with Model Probabilities via Confusion Matrices and Calibration

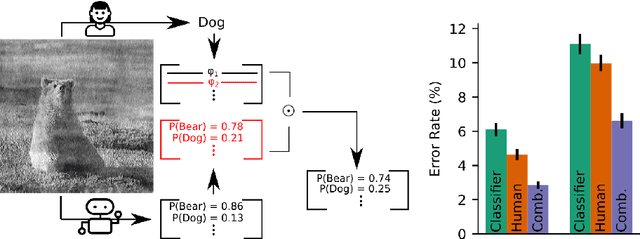
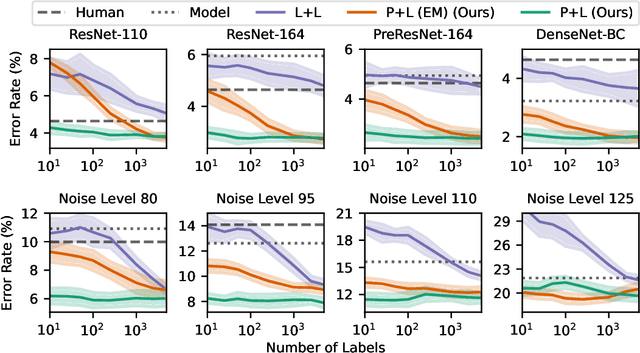
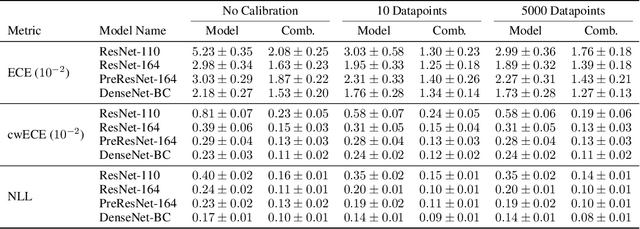
An increasingly common use case for machine learning models is augmenting the abilities of human decision makers. For classification tasks where neither the human or model are perfectly accurate, a key step in obtaining high performance is combining their individual predictions in a manner that leverages their relative strengths. In this work, we develop a set of algorithms that combine the probabilistic output of a model with the class-level output of a human. We show theoretically that the accuracy of our combination model is driven not only by the individual human and model accuracies, but also by the model's confidence. Empirical results on image classification with CIFAR-10 and a subset of ImageNet demonstrate that such human-model combinations consistently have higher accuracies than the model or human alone, and that the parameters of the combination method can be estimated effectively with as few as ten labeled datapoints.

Differentially Private Language Models Benefit from Public Pre-training

Language modeling is a keystone task in natural language processing. When training a language model on sensitive information, differential privacy (DP) allows us to quantify the degree to which our private data is protected. However, training algorithms which enforce differential privacy often lead to degradation in model quality. We study the feasibility of learning a language model which is simultaneously high-quality and privacy preserving by tuning a public base model on a private corpus. We find that DP fine-tuning boosts the performance of language models in the private domain, making the training of such models possible.