Learning deep kernels for exponential family densities

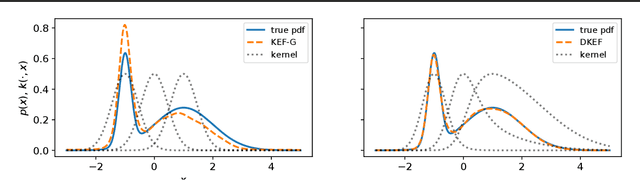
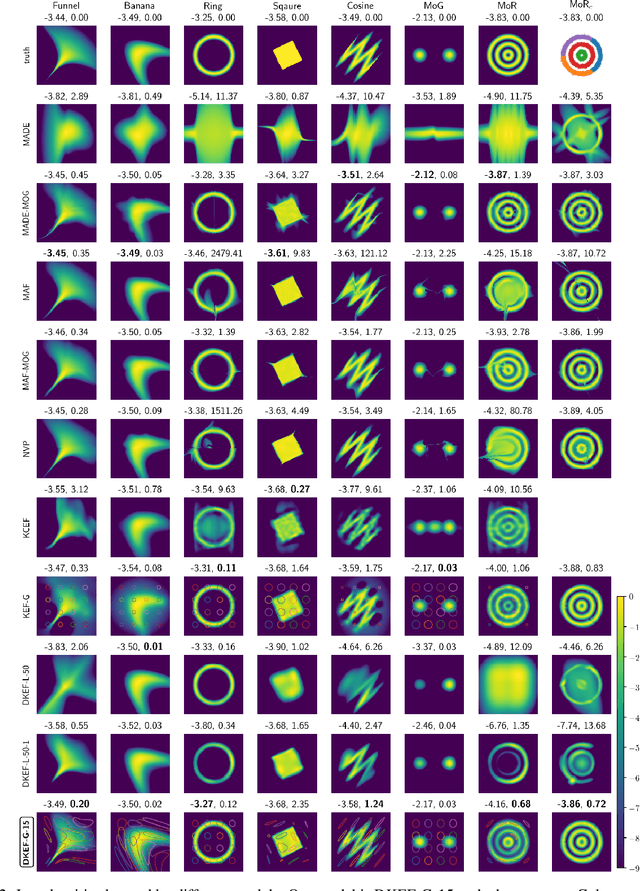
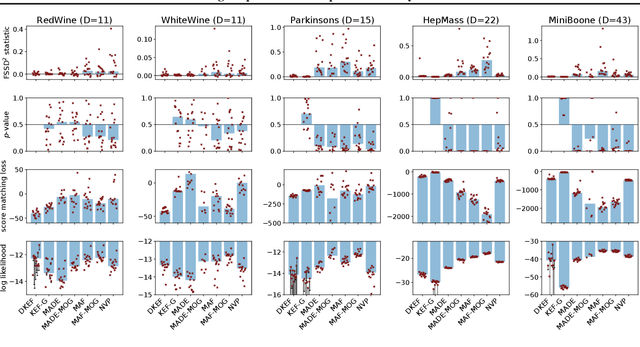
The kernel exponential family is a rich class of distributions,which can be fit efficiently and with statistical guarantees by score matching. Being required to choose a priori a simple kernel such as the Gaussian, however, limits its practical applicability. We provide a scheme for learning a kernel parameterized by a deep network, which can find complex location-dependent local features of the data geometry. This gives a very rich class of density models, capable of fitting complex structures on moderate-dimensional problems. Compared to deep density models fit via maximum likelihood, our approach provides a complementary set of strengths and tradeoffs: in empirical studies, the former can yield higher likelihoods, whereas the latter gives better estimates of the gradient of the log density, the score, which describes the distribution's shape.

Understanding the 2016 US Presidential Election using ecological inference and distribution regression with census microdata

We combine fine-grained spatially referenced census data with the vote outcomes from the 2016 US presidential election. Using this dataset, we perform ecological inference using distribution regression (Flaxman et al, KDD 2015) with a multinomial-logit regression so as to model the vote outcome Trump, Clinton, Other / Didn't vote as a function of demographic and socioeconomic features. Ecological inference allows us to estimate "exit poll" style results like what was Trump's support among white women, but for entirely novel categories. We also perform exploratory data analysis to understand which census variables are predictive of voting for Trump, voting for Clinton, or not voting for either. All of our methods are implemented in python and R and are available online for replication.