Doubly Non-Central Beta Matrix Factorization for DNA Methylation Data
Paper and Code
Jun 12, 2021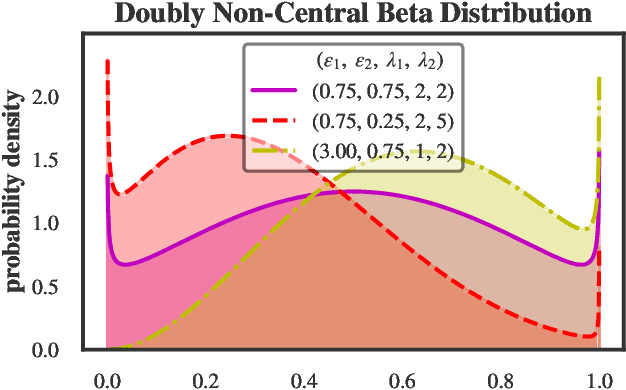
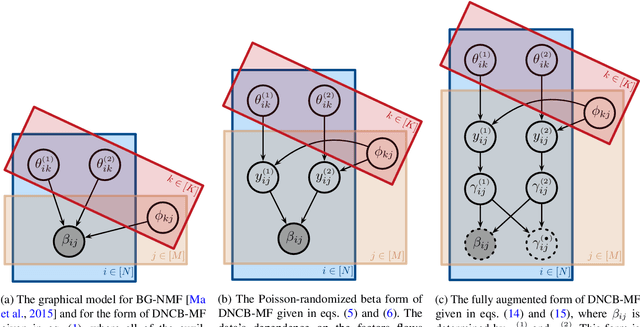

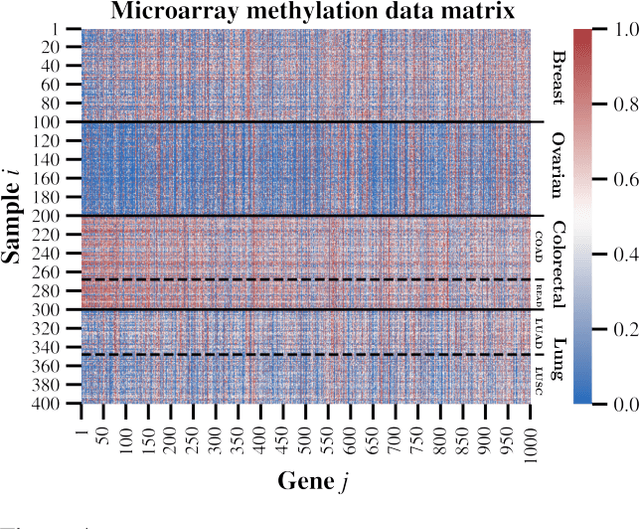
We present a new non-negative matrix factorization model for $(0,1)$ bounded-support data based on the doubly non-central beta (DNCB) distribution, a generalization of the beta distribution. The expressiveness of the DNCB distribution is particularly useful for modeling DNA methylation datasets, which are typically highly dispersed and multi-modal; however, the model structure is sufficiently general that it can be adapted to many other domains where latent representations of $(0,1)$ bounded-support data are of interest. Although the DNCB distribution lacks a closed-form conjugate prior, several augmentations let us derive an efficient posterior inference algorithm composed entirely of analytic updates. Our model improves out-of-sample predictive performance on both real and synthetic DNA methylation datasets over state-of-the-art methods in bioinformatics. In addition, our model yields meaningful latent representations that accord with existing biological knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge