Activation Scaling for Steering and Interpreting Language Models

Given the prompt "Rome is in", can we steer a language model to flip its prediction of an incorrect token "France" to a correct token "Italy" by only multiplying a few relevant activation vectors with scalars? We argue that successfully intervening on a model is a prerequisite for interpreting its internal workings. Concretely, we establish a three-term objective: a successful intervention should flip the correct with the wrong token and vice versa (effectiveness), and leave other tokens unaffected (faithfulness), all while being sparse (minimality). Using gradient-based optimization, this objective lets us learn (and later evaluate) a specific kind of efficient and interpretable intervention: activation scaling only modifies the signed magnitude of activation vectors to strengthen, weaken, or reverse the steering directions already encoded in the model. On synthetic tasks, this intervention performs comparably with steering vectors in terms of effectiveness and faithfulness, but is much more minimal allowing us to pinpoint interpretable model components. We evaluate activation scaling from different angles, compare performance on different datasets, and make activation scalars a learnable function of the activation vectors themselves to generalize to varying-length prompts.

Addressing Discretization-Induced Bias in Demographic Prediction

Racial and other demographic imputation is necessary for many applications, especially in auditing disparities and outreach targeting in political campaigns. The canonical approach is to construct continuous predictions -- e.g., based on name and geography -- and then to $\textit{discretize}$ the predictions by selecting the most likely class (argmax). We study how this practice produces $\textit{discretization bias}$. In particular, we show that argmax labeling, as used by a prominent commercial voter file vendor to impute race/ethnicity, results in a substantial under-count of African-American voters, e.g., by 28.2% points in North Carolina. This bias can have substantial implications in downstream tasks that use such labels. We then introduce a $\textit{joint optimization}$ approach -- and a tractable $\textit{data-driven thresholding}$ heuristic -- that can eliminate this bias, with negligible individual-level accuracy loss. Finally, we theoretically analyze discretization bias, show that calibrated continuous models are insufficient to eliminate it, and that an approach such as ours is necessary. Broadly, we warn researchers and practitioners against discretizing continuous demographic predictions without considering downstream consequences.

Context versus Prior Knowledge in Language Models

To answer a question, language models often need to integrate prior knowledge learned during pretraining and new information presented in context. We hypothesize that models perform this integration in a predictable way across different questions and contexts: models will rely more on prior knowledge for questions about entities (e.g., persons, places, etc.) that they are more familiar with due to higher exposure in the training corpus, and be more easily persuaded by some contexts than others. To formalize this problem, we propose two mutual information-based metrics to measure a model's dependency on a context and on its prior about an entity: first, the persuasion score of a given context represents how much a model depends on the context in its decision, and second, the susceptibility score of a given entity represents how much the model can be swayed away from its original answer distribution about an entity. Following well-established measurement modeling methods, we empirically test for the validity and reliability of these metrics. Finally, we explore and find a relationship between the scores and the model's expected familiarity with an entity, and provide two use cases to illustrate their benefits.

The AL$\ell_0$CORE Tensor Decomposition for Sparse Count Data

This paper introduces AL$\ell_0$CORE, a new form of probabilistic non-negative tensor decomposition. AL$\ell_0$CORE is a Tucker decomposition where the number of non-zero elements (i.e., the $\ell_0$-norm) of the core tensor is constrained to a preset value $Q$ much smaller than the size of the core. While the user dictates the total budget $Q$, the locations and values of the non-zero elements are latent variables and allocated across the core tensor during inference. AL$\ell_0$CORE -- i.e., $allo$cated $\ell_0$-$co$nstrained $core$-- thus enjoys both the computational tractability of CP decomposition and the qualitatively appealing latent structure of Tucker. In a suite of real-data experiments, we demonstrate that AL$\ell_0$CORE typically requires only tiny fractions (e.g.,~1%) of the full core to achieve the same results as full Tucker decomposition at only a correspondingly tiny fraction of the cost.

Measurement in the Age of LLMs: An Application to Ideological Scaling

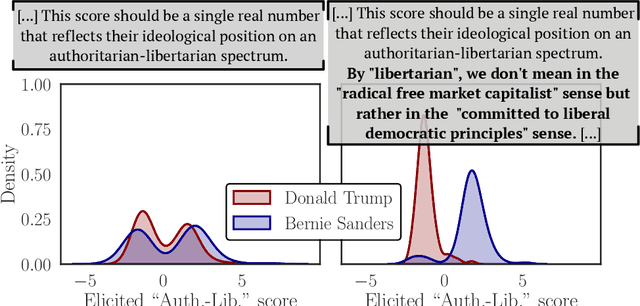
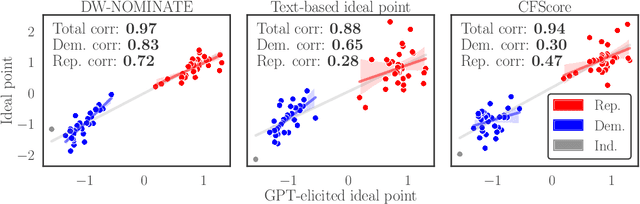
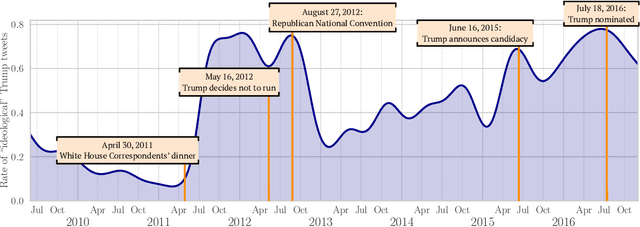
Much of social science is centered around terms like ``ideology'' or ``power'', which generally elude precise definition, and whose contextual meanings are trapped in surrounding language. This paper explores the use of large language models (LLMs) to flexibly navigate the conceptual clutter inherent to social scientific measurement tasks. We rely on LLMs' remarkable linguistic fluency to elicit ideological scales of both legislators and text, which accord closely to established methods and our own judgement. A key aspect of our approach is that we elicit such scores directly, instructing the LLM to furnish numeric scores itself. This approach affords a great deal of flexibility, which we showcase through a variety of different case studies. Our results suggest that LLMs can be used to characterize highly subtle and diffuse manifestations of political ideology in text.

The Ordered Matrix Dirichlet for Modeling Ordinal Dynamics

Many dynamical systems exhibit latent states with intrinsic orderings such as "ally", "neutral" and "enemy" relationships in international relations. Such latent states are evidenced through entities' cooperative versus conflictual interactions which are similarly ordered. Models of such systems often involve state-to-action emission and state-to-state transition matrices. It is common practice to assume that the rows of these stochastic matrices are independently sampled from a Dirichlet distribution. However, this assumption discards ordinal information and treats states and actions falsely as order-invariant categoricals, which hinders interpretation and evaluation. To address this problem, we propose the Ordered Matrix Dirichlet (OMD): rows are sampled conditionally dependent such that probability mass is shifted to the right of the matrix as we move down rows. This results in a well-ordered mapping between latent states and observed action types. We evaluate the OMD in two settings: a Hidden Markov Model and a novel Bayesian Dynamic Poisson Tucker Model tailored to political event data. Models built on the OMD recover interpretable latent states and show superior forecasting performance in few-shot settings. We detail the wide applicability of the OMD to other domains where models with Dirichlet-sampled matrices are popular (e.g. topic modeling) and publish user-friendly code.

An Ordinal Latent Variable Model of Conflict Intensity

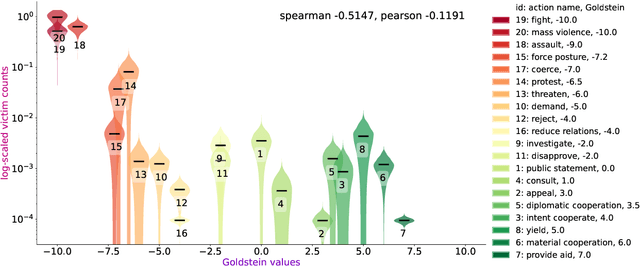
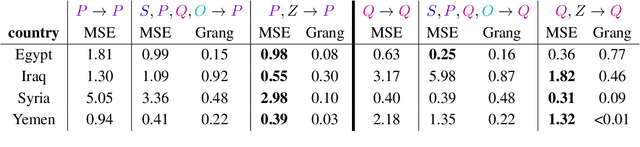
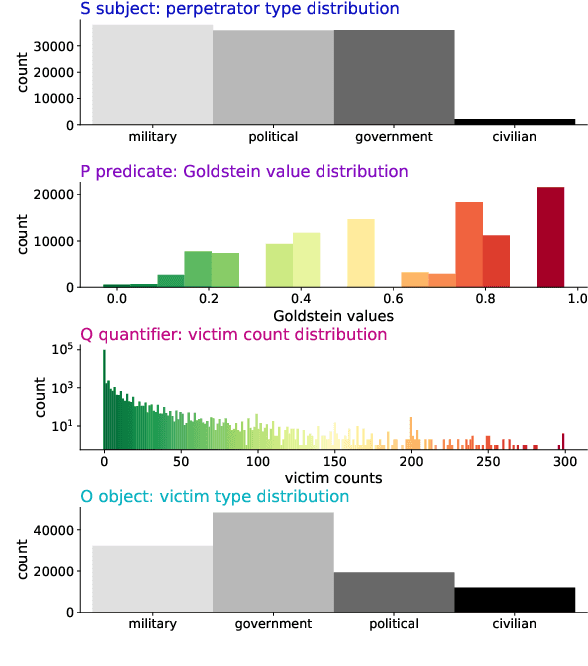
For the quantitative monitoring of international relations, political events are extracted from the news and parsed into "who-did-what-to-whom" patterns. This has resulted in large data collections which require aggregate statistics for analysis. The Goldstein Scale is an expert-based measure that ranks individual events on a one-dimensional scale from conflictual to cooperative. However, the scale disregards fatality counts as well as perpetrator and victim types involved in an event. This information is typically considered in qualitative conflict assessment. To address this limitation, we propose a probabilistic generative model over the full subject-predicate-quantifier-object tuples associated with an event. We treat conflict intensity as an interpretable, ordinal latent variable that correlates conflictual event types with high fatality counts. Taking a Bayesian approach, we learn a conflict intensity scale from data and find the optimal number of intensity classes. We evaluate the model by imputing missing data. Our scale proves to be more informative than the original Goldstein Scale in autoregressive forecasting and when compared with global online attention towards armed conflicts.

Doubly Non-Central Beta Matrix Factorization for DNA Methylation Data

We present a new non-negative matrix factorization model for $(0,1)$ bounded-support data based on the doubly non-central beta (DNCB) distribution, a generalization of the beta distribution. The expressiveness of the DNCB distribution is particularly useful for modeling DNA methylation datasets, which are typically highly dispersed and multi-modal; however, the model structure is sufficiently general that it can be adapted to many other domains where latent representations of $(0,1)$ bounded-support data are of interest. Although the DNCB distribution lacks a closed-form conjugate prior, several augmentations let us derive an efficient posterior inference algorithm composed entirely of analytic updates. Our model improves out-of-sample predictive performance on both real and synthetic DNA methylation datasets over state-of-the-art methods in bioinformatics. In addition, our model yields meaningful latent representations that accord with existing biological knowledge.

Poisson-Randomized Gamma Dynamical Systems

This paper presents the Poisson-randomized gamma dynamical system (PRGDS), a model for sequentially observed count tensors that encodes a strong inductive bias toward sparsity and burstiness. The PRGDS is based on a new motif in Bayesian latent variable modeling, an alternating chain of discrete Poisson and continuous gamma latent states that is analytically convenient and computationally tractable. This motif yields closed-form complete conditionals for all variables by way of the Bessel distribution and a novel discrete distribution that we call the shifted confluent hypergeometric distribution. We draw connections to closely related models and compare the PRGDS to these models in studies of real-world count data sets of text, international events, and neural spike trains. We find that a sparse variant of the PRGDS, which allows the continuous gamma latent states to take values of exactly zero, often obtains better predictive performance than other models and is uniquely capable of inferring latent structures that are highly localized in time.

Locally Private Bayesian Inference for Count Models

As more aspects of social interaction are digitally recorded, there is a growing need to develop privacy-preserving data analysis methods. Social scientists will be more likely to adopt these methods if doing so entails minimal change to their current methodology. Toward that end, we present a general and modular method for privatizing Bayesian inference for Poisson factorization, a broad class of models that contains some of the most widely used models in the social sciences. Our method satisfies local differential privacy, which ensures that no single centralized server need ever store the non-privatized data. To formulate our local-privacy guarantees, we introduce and focus on limited-precision local privacy---the local privacy analog of limited-precision differential privacy (Flood et al., 2013). We present two case studies, one involving social networks and one involving text corpora, that test our method's ability to form the posterior distribution over latent variables under different levels of noise, and demonstrate our method's utility over a na\"{i}ve approach, wherein inference proceeds as usual, treating the privatized data as if it were not privatized.