A study of animal action segmentation algorithms across supervised, unsupervised, and semi-supervised learning paradigms

Action segmentation of behavioral videos is the process of labeling each frame as belonging to one or more discrete classes, and is a crucial component of many studies that investigate animal behavior. A wide range of algorithms exist to automatically parse discrete animal behavior, encompassing supervised, unsupervised, and semi-supervised learning paradigms. These algorithms -- which include tree-based models, deep neural networks, and graphical models -- differ widely in their structure and assumptions on the data. Using four datasets spanning multiple species -- fly, mouse, and human -- we systematically study how the outputs of these various algorithms align with manually annotated behaviors of interest. Along the way, we introduce a semi-supervised action segmentation model that bridges the gap between supervised deep neural networks and unsupervised graphical models. We find that fully supervised temporal convolutional networks with the addition of temporal information in the observations perform the best on our supervised metrics across all datasets.

Towards a "universal translator" for neural dynamics at single-cell, single-spike resolution

Neuroscience research has made immense progress over the last decade, but our understanding of the brain remains fragmented and piecemeal: the dream of probing an arbitrary brain region and automatically reading out the information encoded in its neural activity remains out of reach. In this work, we build towards a first foundation model for neural spiking data that can solve a diverse set of tasks across multiple brain areas. We introduce a novel self-supervised modeling approach for population activity in which the model alternates between masking out and reconstructing neural activity across different time steps, neurons, and brain regions. To evaluate our approach, we design unsupervised and supervised prediction tasks using the International Brain Laboratory repeated site dataset, which is comprised of Neuropixels recordings targeting the same brain locations across 48 animals and experimental sessions. The prediction tasks include single-neuron and region-level activity prediction, forward prediction, and behavior decoding. We demonstrate that our multi-task-masking (MtM) approach significantly improves the performance of current state-of-the-art population models and enables multi-task learning. We also show that by training on multiple animals, we can improve the generalization ability of the model to unseen animals, paving the way for a foundation model of the brain at single-cell, single-spike resolution.

SemiMultiPose: A Semi-supervised Multi-animal Pose Estimation Framework

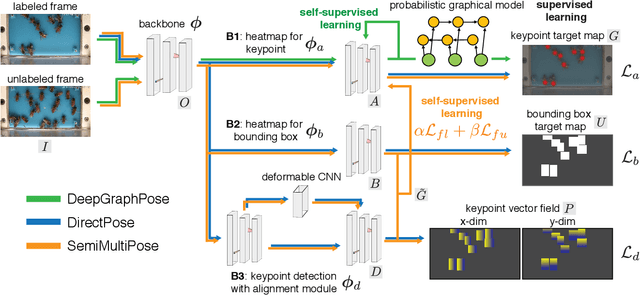
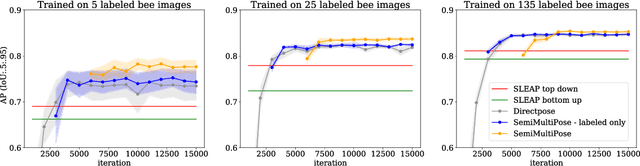
Multi-animal pose estimation is essential for studying animals' social behaviors in neuroscience and neuroethology. Advanced approaches have been proposed to support multi-animal estimation and achieve state-of-the-art performance. However, these models rarely exploit unlabeled data during training even though real world applications have exponentially more unlabeled frames than labeled frames. Manually adding dense annotations for a large number of images or videos is costly and labor-intensive, especially for multiple instances. Given these deficiencies, we propose a novel semi-supervised architecture for multi-animal pose estimation, leveraging the abundant structures pervasive in unlabeled frames in behavior videos to enhance training, which is critical for sparsely-labeled problems. The resulting algorithm will provide superior multi-animal pose estimation results on three animal experiments compared to the state-of-the-art baseline and exhibits more predictive power in sparsely-labeled data regimes.

Attentive Clustering Processes

Amortized approaches to clustering have recently received renewed attention thanks to novel objective functions that exploit the expressiveness of deep learning models. In this work we revisit a recent proposal for fast amortized probabilistic clustering, the Clusterwise Clustering Process (CCP), which yields samples from the posterior distribution of cluster labels for sets of arbitrary size using only O(K) forward network evaluations, where K is an arbitrary number of clusters. While adequate in simple datasets, we show that the model can severely underfit complex datasets, and hypothesize that this limitation can be traced back to the implicit assumption that the probability of a point joining a cluster is equally sensitive to all the points available to join the same cluster. We propose an improved model, the Attentive Clustering Process (ACP), that selectively pays more attention to relevant points while preserving the invariance properties of the generative model. We illustrate the advantages of the new model in applications to spike-sorting in multi-electrode arrays and community discovery in networks. The latter case combines the ACP model with graph convolutional networks, and to our knowledge is the first deep learning model that handles an arbitrary number of communities.

A zero-inflated gamma model for deconvolved calcium imaging traces

Calcium imaging is a critical tool for measuring the activity of large neural populations. Much effort has been devoted to developing "pre-processing" tools for calcium video data, addressing the important issues of e.g., motion correction, denoising, compression, demixing, and deconvolution. However, statistical modeling of deconvolved calcium signals (i.e., the estimated activity extracted by a pre-processing pipeline) is just as critical for interpreting calcium measurements, and for incorporating these observations into downstream probabilistic encoding and decoding models. Surprisingly, these issues have to date received significantly less attention. In this work we examine the statistical properties of the deconvolved activity estimates, and compare probabilistic models for these random signals. In particular, we propose a zero-inflated gamma (ZIG) model, which characterizes the calcium responses as a mixture of a gamma distribution and a point mass that serves to model zero responses. We apply the resulting models to neural encoding and decoding problems. We find that the ZIG model outperforms simpler models (e.g., Poisson or Bernoulli models) in the context of both simulated and real neural data, and can therefore play a useful role in bridging calcium imaging analysis methods with tools for analyzing activity in large neural populations.

Disentangled sticky hierarchical Dirichlet process hidden Markov model

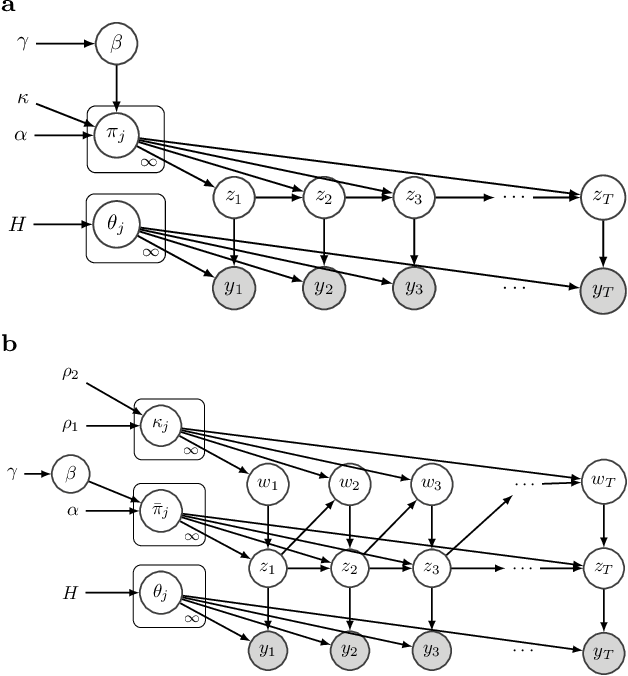
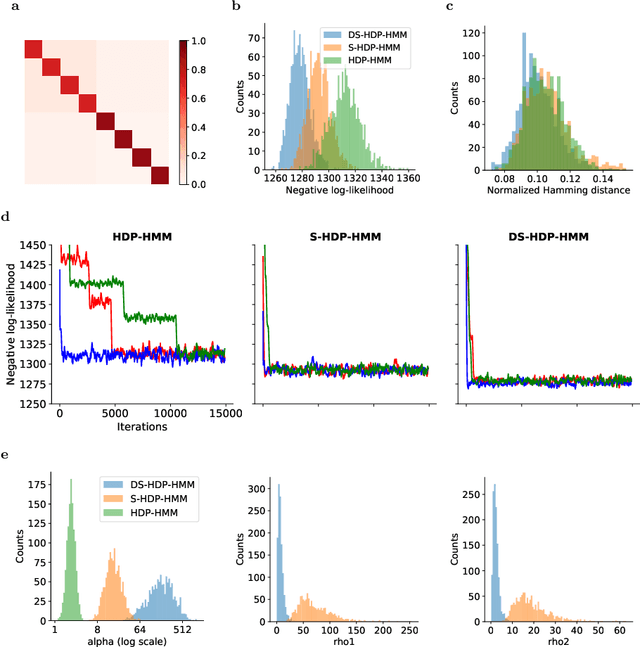
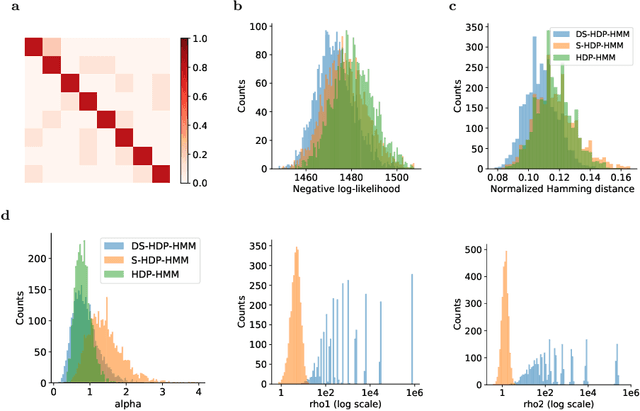
The Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) has been used widely as a natural Bayesian nonparametric extension of the classical Hidden Markov Model for learning from sequential and time-series data. A sticky extension of the HDP-HMM has been proposed to strengthen the self-persistence probability in the HDP-HMM. However, the sticky HDP-HMM entangles the strength of the self-persistence prior and transition prior together, limiting its expressiveness. Here, we propose a more general model: the disentangled sticky HDP-HMM (DS-HDP-HMM). We develop novel Gibbs sampling algorithms for efficient inference in this model. We show that the disentangled sticky HDP-HMM outperforms the sticky HDP-HMM and HDP-HMM on both synthetic and real data, and apply the new approach to analyze neural data and segment behavioral video data.

General linear-time inference for Gaussian Processes on one dimension

Gaussian Processes (GPs) provide a powerful probabilistic framework for interpolation, forecasting, and smoothing, but have been hampered by computational scaling issues. Here we prove that for data sampled on one dimension (e.g., a time series sampled at arbitrarily-spaced intervals), approximate GP inference at any desired level of accuracy requires computational effort that scales linearly with the number of observations; this new theorem enables inference on much larger datasets than was previously feasible. To achieve this improved scaling we propose a new family of stationary covariance kernels: the Latent Exponentially Generated (LEG) family, which admits a convenient stable state-space representation that allows linear-time inference. We prove that any continuous integrable stationary kernel can be approximated arbitrarily well by some member of the LEG family. The proof draws connections to Spectral Mixture Kernels, providing new insight about the flexibility of this popular family of kernels. We propose parallelized algorithms for performing inference and learning in the LEG model, test the algorithm on real and synthetic data, and demonstrate scaling to datasets with billions of samples.

Discrete Neural Processes

Many data generating processes involve latent random variables over discrete combinatorial spaces whose size grows factorially with the dataset. In these settings, existing posterior inference methods can be inaccurate and/or very slow. In this work we develop methods for efficient amortized approximate Bayesian inference over discrete combinatorial spaces, with applications to random permutations, probabilistic clustering (such as Dirichlet process mixture models) and random communities (such as stochastic block models). The approach is based on mapping distributed, symmetry-invariant representations of discrete arrangements into conditional probabilities. The resulting algorithms parallelize easily, yield iid samples from the approximate posteriors, and can easily be applied to both conjugate and non-conjugate models, as training only requires samples from the generative model.

Amortized Bayesian inference for clustering models

We develop methods for efficient amortized approximate Bayesian inference over posterior distributions of probabilistic clustering models, such as Dirichlet process mixture models. The approach is based on mapping distributed, symmetry-invariant representations of cluster arrangements into conditional probabilities. The method parallelizes easily, yields iid samples from the approximate posterior of cluster assignments with the same computational cost of a single Gibbs sampler sweep, and can easily be applied to both conjugate and non-conjugate models, as training only requires samples from the generative model.

A Novel Variational Family for Hidden Nonlinear Markov Models

Latent variable models have been widely applied for the analysis and visualization of large datasets. In the case of sequential data, closed-form inference is possible when the transition and observation functions are linear. However, approximate inference techniques are usually necessary when dealing with nonlinear dynamics and observation functions. Here, we propose a novel variational inference framework for the explicit modeling of time series, Variational Inference for Nonlinear Dynamics (VIND), that is able to uncover nonlinear observation and transition functions from sequential data. The framework includes a structured approximate posterior, and an algorithm that relies on the fixed-point iteration method to find the best estimate for latent trajectories. We apply the method to several datasets and show that it is able to accurately infer the underlying dynamics of these systems, in some cases substantially outperforming state-of-the-art methods.