An Investigation of Conformal Isometry Hypothesis for Grid Cells

This paper investigates the conformal isometry hypothesis as a potential explanation for the emergence of hexagonal periodic patterns in the response maps of grid cells. The hypothesis posits that the activities of the population of grid cells form a high-dimensional vector in the neural space, representing the agent's self-position in 2D physical space. As the agent moves in the 2D physical space, the vector rotates in a 2D manifold in the neural space, driven by a recurrent neural network. The conformal isometry hypothesis proposes that this 2D manifold in the neural space is a conformally isometric embedding of the 2D physical space, in the sense that local displacements of the vector in neural space are proportional to local displacements of the agent in the physical space. Thus the 2D manifold forms an internal map of the 2D physical space, equipped with an internal metric. In this paper, we conduct numerical experiments to show that this hypothesis underlies the hexagon periodic patterns of grid cells. We also conduct theoretical analysis to further support this hypothesis. In addition, we propose a conformal modulation of the input velocity of the agent so that the recurrent neural network of grid cells satisfies the conformal isometry hypothesis automatically. To summarize, our work provides numerical and theoretical evidences for the conformal isometry hypothesis for grid cells and may serve as a foundation for further development of normative models of grid cells and beyond.

Conformal Normalization in Recurrent Neural Network of Grid Cells

Grid cells in the entorhinal cortex of the mammalian brain exhibit striking hexagon firing patterns in their response maps as the animal (e.g., a rat) navigates in a 2D open environment. The responses of the population of grid cells collectively form a vector in a high-dimensional neural activity space, and this vector represents the self-position of the agent in the 2D physical space. As the agent moves, the vector is transformed by a recurrent neural network that takes the velocity of the agent as input. In this paper, we propose a simple and general conformal normalization of the input velocity for the recurrent neural network, so that the local displacement of the position vector in the high-dimensional neural space is proportional to the local displacement of the agent in the 2D physical space, regardless of the direction of the input velocity. Our numerical experiments on the minimally simple linear and non-linear recurrent networks show that conformal normalization leads to the emergence of the hexagon grid patterns. Furthermore, we derive a new theoretical understanding that connects conformal normalization to the emergence of hexagon grid patterns in navigation tasks.

Conformal Isometry of Lie Group Representation in Recurrent Network of Grid Cells

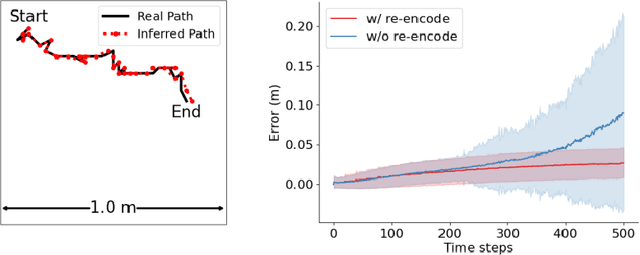
The activity of the grid cell population in the medial entorhinal cortex (MEC) of the brain forms a vector representation of the self-position of the animal. Recurrent neural networks have been developed to explain the properties of the grid cells by transforming the vector based on the input velocity, so that the grid cells can perform path integration. In this paper, we investigate the algebraic, geometric, and topological properties of grid cells using recurrent network models. Algebraically, we study the Lie group and Lie algebra of the recurrent transformation as a representation of self-motion. Geometrically, we study the conformal isometry of the Lie group representation of the recurrent network where the local displacement of the vector in the neural space is proportional to the local displacement of the agent in the 2D physical space. We then focus on a simple non-linear recurrent model that underlies the continuous attractor neural networks of grid cells. Our numerical experiments show that conformal isometry leads to hexagon periodic patterns of the response maps of grid cells and our model is capable of accurate path integration.

Learning identifiable and interpretable latent models of high-dimensional neural activity using pi-VAE

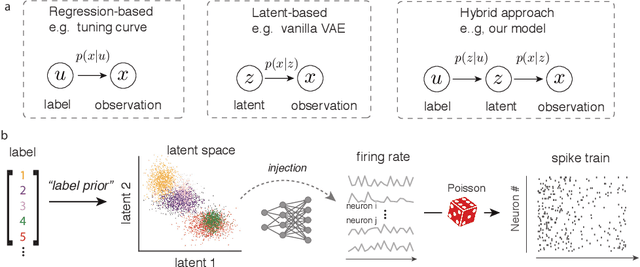
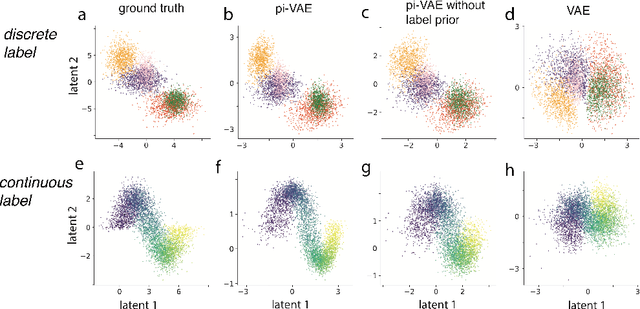
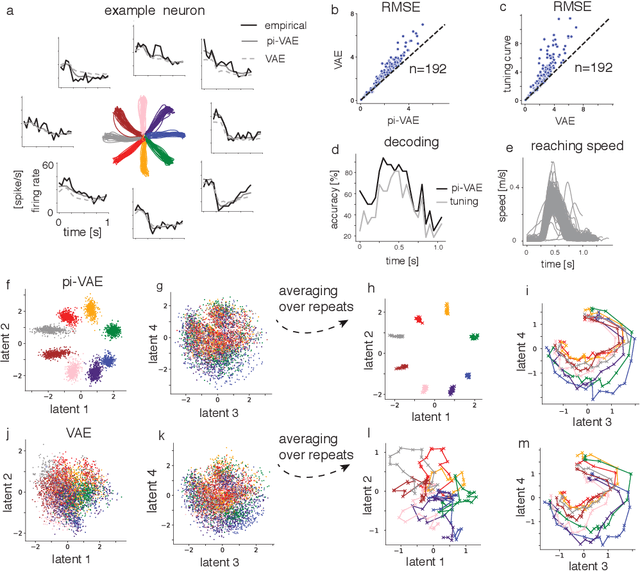
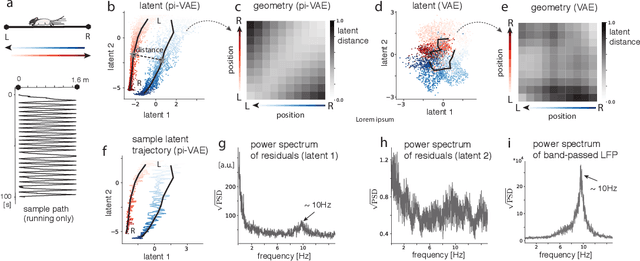
The ability to record activities from hundreds of neurons simultaneously in the brain has placed an increasing demand for developing appropriate statistical techniques to analyze such data. Recently, deep generative models have been proposed to fit neural population responses. While these methods are flexible and expressive, the downside is that they can be difficult to interpret and identify. To address this problem, we propose a method that integrates key ingredients from latent models and traditional neural encoding models. Our method, pi-VAE, is inspired by recent progress on identifiable variational auto-encoder, which we adapt to make appropriate for neuroscience applications. Specifically, we propose to construct latent variable models of neural activity while simultaneously modeling the relation between the latent and task variables (non-neural variables, e.g. sensory, motor, and other externally observable states). The incorporation of task variables results in models that are not only more constrained, but also show qualitative improvements in interpretability and identifiability. We validate pi-VAE using synthetic data, and apply it to analyze neurophysiological datasets from rat hippocampus and macaque motor cortex. We demonstrate that pi-VAE not only fits the data better, but also provides unexpected novel insights into the structure of the neural codes.

A zero-inflated gamma model for deconvolved calcium imaging traces

Calcium imaging is a critical tool for measuring the activity of large neural populations. Much effort has been devoted to developing "pre-processing" tools for calcium video data, addressing the important issues of e.g., motion correction, denoising, compression, demixing, and deconvolution. However, statistical modeling of deconvolved calcium signals (i.e., the estimated activity extracted by a pre-processing pipeline) is just as critical for interpreting calcium measurements, and for incorporating these observations into downstream probabilistic encoding and decoding models. Surprisingly, these issues have to date received significantly less attention. In this work we examine the statistical properties of the deconvolved activity estimates, and compare probabilistic models for these random signals. In particular, we propose a zero-inflated gamma (ZIG) model, which characterizes the calcium responses as a mixture of a gamma distribution and a point mass that serves to model zero responses. We apply the resulting models to neural encoding and decoding problems. We find that the ZIG model outperforms simpler models (e.g., Poisson or Bernoulli models) in the context of both simulated and real neural data, and can therefore play a useful role in bridging calcium imaging analysis methods with tools for analyzing activity in large neural populations.

Emergence of functional and structural properties of the head direction system by optimization of recurrent neural networks

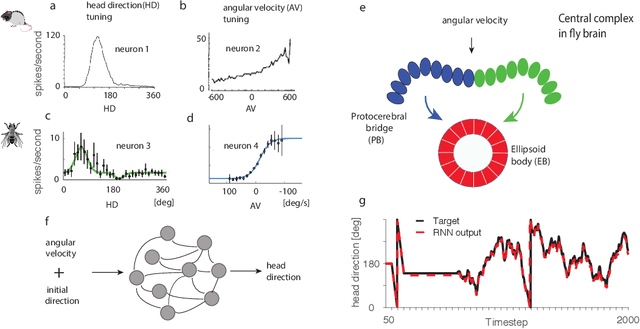
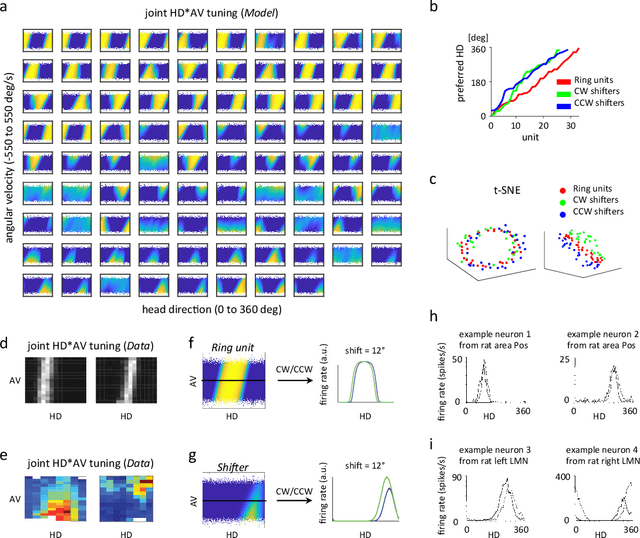
Recent work suggests goal-driven training of neural networks can be used to model neural activity in the brain. While response properties of neurons in artificial neural networks bear similarities to those in the brain, the network architectures are often constrained to be different. Here we ask if a neural network can recover both neural representations and, if the architecture is unconstrained and optimized, the anatomical properties of neural circuits. We demonstrate this in a system where the connectivity and the functional organization have been characterized, namely, the head direction circuits of the rodent and fruit fly. We trained recurrent neural networks (RNNs) to estimate head direction through integration of angular velocity. We found that the two distinct classes of neurons observed in the head direction system, the Ring neurons and the Shifter neurons, emerged naturally in artificial neural networks as a result of training. Furthermore, connectivity analysis and in-silico neurophysiology revealed structural and mechanistic similarities between artificial networks and the head direction system. Overall, our results show that optimization of RNNs in a goal-driven task can recapitulate the structure and function of biological circuits, suggesting that artificial neural networks can be used to study the brain at the level of both neural activity and anatomical organization.

Emergence of grid-like representations by training recurrent neural networks to perform spatial localization

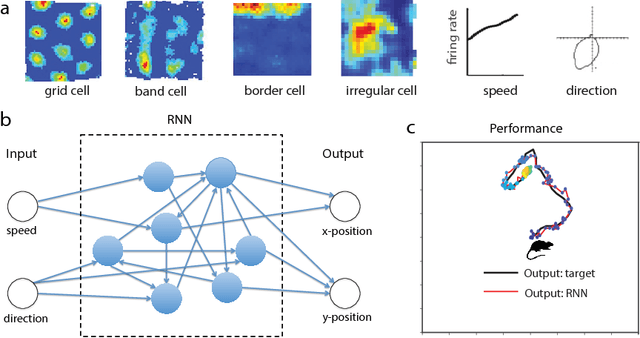
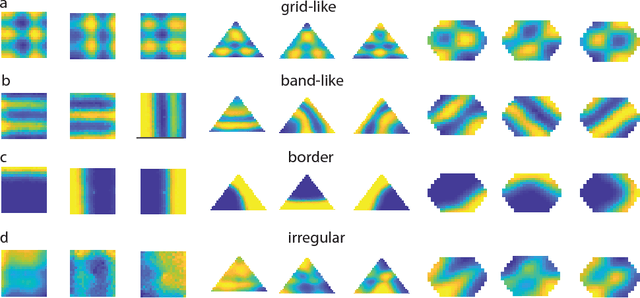
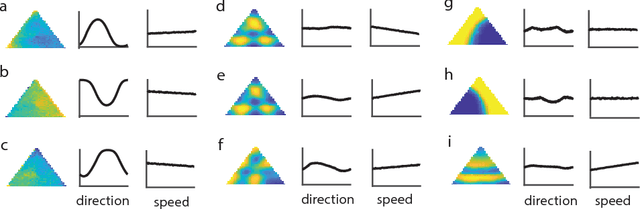
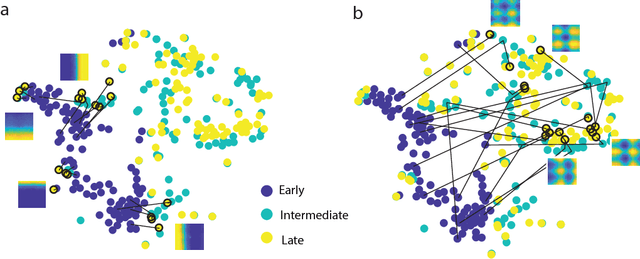
Decades of research on the neural code underlying spatial navigation have revealed a diverse set of neural response properties. The Entorhinal Cortex (EC) of the mammalian brain contains a rich set of spatial correlates, including grid cells which encode space using tessellating patterns. However, the mechanisms and functional significance of these spatial representations remain largely mysterious. As a new way to understand these neural representations, we trained recurrent neural networks (RNNs) to perform navigation tasks in 2D arenas based on velocity inputs. Surprisingly, we find that grid-like spatial response patterns emerge in trained networks, along with units that exhibit other spatial correlates, including border cells and band-like cells. All these different functional types of neurons have been observed experimentally. The order of the emergence of grid-like and border cells is also consistent with observations from developmental studies. Together, our results suggest that grid cells, border cells and others as observed in EC may be a natural solution for representing space efficiently given the predominant recurrent connections in the neural circuits.