A minimalistic representation model for head direction system

We present a minimalistic representation model for the head direction (HD) system, aiming to learn a high-dimensional representation of head direction that captures essential properties of HD cells. Our model is a representation of rotation group $U(1)$, and we study both the fully connected version and convolutional version. We demonstrate the emergence of Gaussian-like tuning profiles and a 2D circle geometry in both versions of the model. We also demonstrate that the learned model is capable of accurate path integration.

An Investigation of Conformal Isometry Hypothesis for Grid Cells

This paper investigates the conformal isometry hypothesis as a potential explanation for the emergence of hexagonal periodic patterns in the response maps of grid cells. The hypothesis posits that the activities of the population of grid cells form a high-dimensional vector in the neural space, representing the agent's self-position in 2D physical space. As the agent moves in the 2D physical space, the vector rotates in a 2D manifold in the neural space, driven by a recurrent neural network. The conformal isometry hypothesis proposes that this 2D manifold in the neural space is a conformally isometric embedding of the 2D physical space, in the sense that local displacements of the vector in neural space are proportional to local displacements of the agent in the physical space. Thus the 2D manifold forms an internal map of the 2D physical space, equipped with an internal metric. In this paper, we conduct numerical experiments to show that this hypothesis underlies the hexagon periodic patterns of grid cells. We also conduct theoretical analysis to further support this hypothesis. In addition, we propose a conformal modulation of the input velocity of the agent so that the recurrent neural network of grid cells satisfies the conformal isometry hypothesis automatically. To summarize, our work provides numerical and theoretical evidences for the conformal isometry hypothesis for grid cells and may serve as a foundation for further development of normative models of grid cells and beyond.

Conformal Normalization in Recurrent Neural Network of Grid Cells

Grid cells in the entorhinal cortex of the mammalian brain exhibit striking hexagon firing patterns in their response maps as the animal (e.g., a rat) navigates in a 2D open environment. The responses of the population of grid cells collectively form a vector in a high-dimensional neural activity space, and this vector represents the self-position of the agent in the 2D physical space. As the agent moves, the vector is transformed by a recurrent neural network that takes the velocity of the agent as input. In this paper, we propose a simple and general conformal normalization of the input velocity for the recurrent neural network, so that the local displacement of the position vector in the high-dimensional neural space is proportional to the local displacement of the agent in the 2D physical space, regardless of the direction of the input velocity. Our numerical experiments on the minimally simple linear and non-linear recurrent networks show that conformal normalization leads to the emergence of the hexagon grid patterns. Furthermore, we derive a new theoretical understanding that connects conformal normalization to the emergence of hexagon grid patterns in navigation tasks.

Conformal Isometry of Lie Group Representation in Recurrent Network of Grid Cells

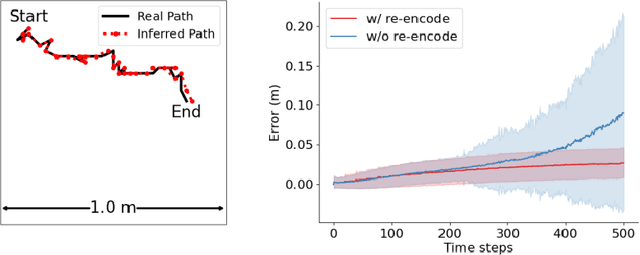
The activity of the grid cell population in the medial entorhinal cortex (MEC) of the brain forms a vector representation of the self-position of the animal. Recurrent neural networks have been developed to explain the properties of the grid cells by transforming the vector based on the input velocity, so that the grid cells can perform path integration. In this paper, we investigate the algebraic, geometric, and topological properties of grid cells using recurrent network models. Algebraically, we study the Lie group and Lie algebra of the recurrent transformation as a representation of self-motion. Geometrically, we study the conformal isometry of the Lie group representation of the recurrent network where the local displacement of the vector in the neural space is proportional to the local displacement of the agent in the 2D physical space. We then focus on a simple non-linear recurrent model that underlies the continuous attractor neural networks of grid cells. Our numerical experiments show that conformal isometry leads to hexagon periodic patterns of the response maps of grid cells and our model is capable of accurate path integration.

SurfGen: Adversarial 3D Shape Synthesis with Explicit Surface Discriminators

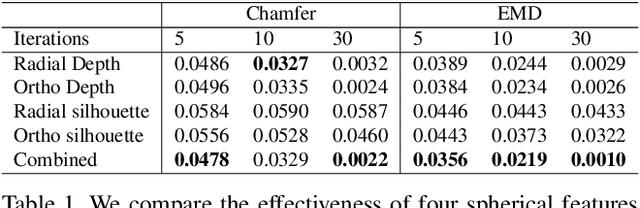
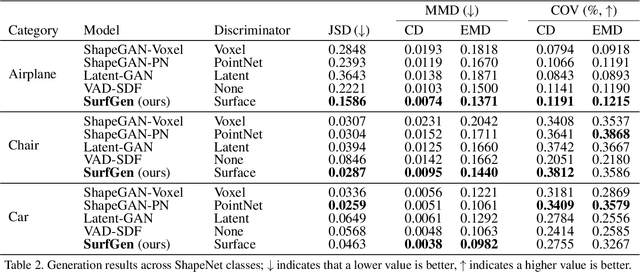
Recent advances in deep generative models have led to immense progress in 3D shape synthesis. While existing models are able to synthesize shapes represented as voxels, point-clouds, or implicit functions, these methods only indirectly enforce the plausibility of the final 3D shape surface. Here we present a 3D shape synthesis framework (SurfGen) that directly applies adversarial training to the object surface. Our approach uses a differentiable spherical projection layer to capture and represent the explicit zero isosurface of an implicit 3D generator as functions defined on the unit sphere. By processing the spherical representation of 3D object surfaces with a spherical CNN in an adversarial setting, our generator can better learn the statistics of natural shape surfaces. We evaluate our model on large-scale shape datasets, and demonstrate that the end-to-end trained model is capable of generating high fidelity 3D shapes with diverse topology.