Boosting Semi-Supervised Medical Image Segmentation via Masked Image Consistency and Discrepancy Learning

Semi-supervised learning is of great significance in medical image segmentation by exploiting unlabeled data. Among its strategies, the co-training framework is prominent. However, previous co-training studies predominantly concentrate on network initialization variances and pseudo-label generation, while overlooking the equilibrium between information interchange and model diversity preservation. In this paper, we propose the Masked Image Consistency and Discrepancy Learning (MICD) framework with three key modules. The Masked Cross Pseudo Consistency (MCPC) module enriches context perception and small sample learning via pseudo-labeling across masked-input branches. The Cross Feature Consistency (CFC) module fortifies information exchange and model robustness by ensuring decoder feature consistency. The Cross Model Discrepancy (CMD) module utilizes EMA teacher networks to oversee outputs and preserve branch diversity. Together, these modules address existing limitations by focusing on fine-grained local information and maintaining diversity in a heterogeneous framework. Experiments on two public medical image datasets, AMOS and Synapse, demonstrate that our approach outperforms state-of-the-art methods.

Privacy-Aware RAG: Secure and Isolated Knowledge Retrieval

The widespread adoption of Retrieval-Augmented Generation (RAG) systems in real-world applications has heightened concerns about the confidentiality and integrity of their proprietary knowledge bases. These knowledge bases, which play a critical role in enhancing the generative capabilities of Large Language Models (LLMs), are increasingly vulnerable to breaches that could compromise sensitive information. To address these challenges, this paper proposes an advanced encryption methodology designed to protect RAG systems from unauthorized access and data leakage. Our approach encrypts both textual content and its corresponding embeddings prior to storage, ensuring that all data remains securely encrypted. This mechanism restricts access to authorized entities with the appropriate decryption keys, thereby significantly reducing the risk of unintended data exposure. Furthermore, we demonstrate that our encryption strategy preserves the performance and functionality of RAG pipelines, ensuring compatibility across diverse domains and applications. To validate the robustness of our method, we provide comprehensive security proofs that highlight its resilience against potential threats and vulnerabilities. These proofs also reveal limitations in existing approaches, which often lack robustness, adaptability, or reliance on open-source models. Our findings suggest that integrating advanced encryption techniques into the design and deployment of RAG systems can effectively enhance privacy safeguards. This research contributes to the ongoing discourse on improving security measures for AI-driven services and advocates for stricter data protection standards within RAG architectures.

Efficient Streaming Voice Steganalysis in Challenging Detection Scenarios

In recent years, there has been an increasing number of information hiding techniques based on network streaming media, focusing on how to covertly and efficiently embed secret information into real-time transmitted network media signals to achieve concealed communication. The misuse of these techniques can lead to significant security risks, such as the spread of malicious code, commands, and viruses. Current steganalysis methods for network voice streams face two major challenges: efficient detection under low embedding rates and short duration conditions. These challenges arise because, with low embedding rates (e.g., as low as 10%) and short transmission durations (e.g., only 0.1 second), detection models struggle to acquire sufficiently rich sample features, making effective steganalysis difficult. To address these challenges, this paper introduces a Dual-View VoIP Steganalysis Framework (DVSF). The framework first randomly obfuscates parts of the native steganographic descriptors in VoIP stream segments, making the steganographic features of hard-to-detect samples more pronounced and easier to learn. It then captures fine-grained local features related to steganography, building on the global features of VoIP. Specially constructed VoIP segment triplets further adjust the feature distances within the model. Ultimately, this method effectively address the detection difficulty in VoIP. Extensive experiments demonstrate that our method significantly improves the accuracy of streaming voice steganalysis in these challenging detection scenarios, surpassing existing state-of-the-art methods and offering superior near-real-time performance.

Monotonic Neural Network: combining Deep Learning with Domain Knowledge for Chiller Plants Energy Optimization

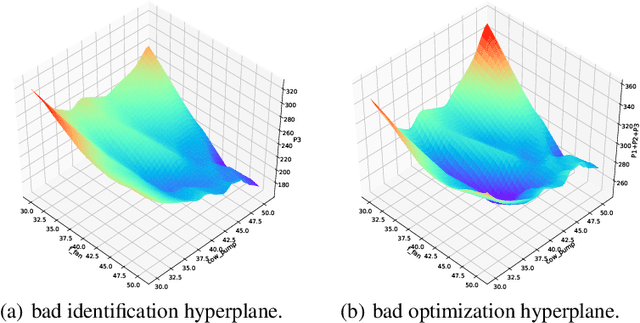
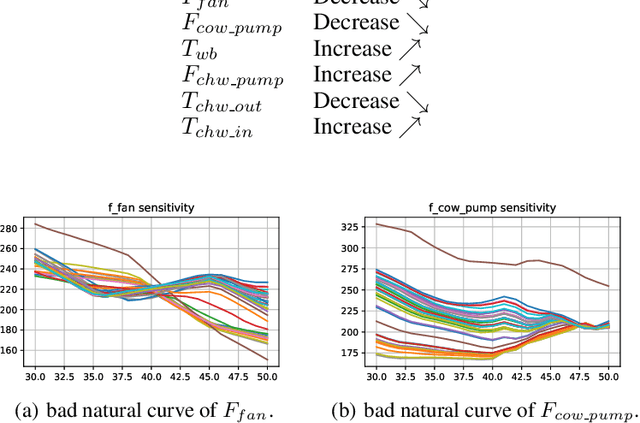
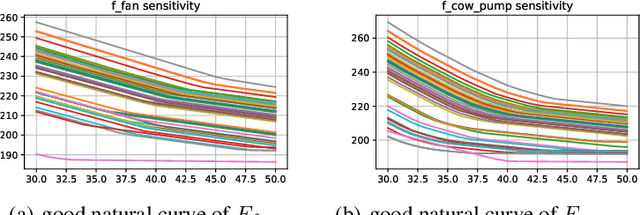
In this paper, we are interested in building a domain knowledge based deep learning framework to solve the chiller plants energy optimization problems. Compared to the hotspot applications of deep learning (e.g. image classification and NLP), it is difficult to collect enormous data for deep network training in real-world physical systems. Most existing methods reduce the complex systems into linear model to facilitate the training on small samples. To tackle the small sample size problem, this paper considers domain knowledge in the structure and loss design of deep network to build a nonlinear model with lower redundancy function space. Specifically, the energy consumption estimation of most chillers can be physically viewed as an input-output monotonic problem. Thus, we can design a Neural Network with monotonic constraints to mimic the physical behavior of the system. We verify the proposed method in a cooling system of a data center, experimental results show the superiority of our framework in energy optimization compared to the existing ones.

A zero-inflated gamma model for deconvolved calcium imaging traces

Calcium imaging is a critical tool for measuring the activity of large neural populations. Much effort has been devoted to developing "pre-processing" tools for calcium video data, addressing the important issues of e.g., motion correction, denoising, compression, demixing, and deconvolution. However, statistical modeling of deconvolved calcium signals (i.e., the estimated activity extracted by a pre-processing pipeline) is just as critical for interpreting calcium measurements, and for incorporating these observations into downstream probabilistic encoding and decoding models. Surprisingly, these issues have to date received significantly less attention. In this work we examine the statistical properties of the deconvolved activity estimates, and compare probabilistic models for these random signals. In particular, we propose a zero-inflated gamma (ZIG) model, which characterizes the calcium responses as a mixture of a gamma distribution and a point mass that serves to model zero responses. We apply the resulting models to neural encoding and decoding problems. We find that the ZIG model outperforms simpler models (e.g., Poisson or Bernoulli models) in the context of both simulated and real neural data, and can therefore play a useful role in bridging calcium imaging analysis methods with tools for analyzing activity in large neural populations.

Dynamic Connected Neural Decision Classifier and Regressor with Dynamic Softing Pruning

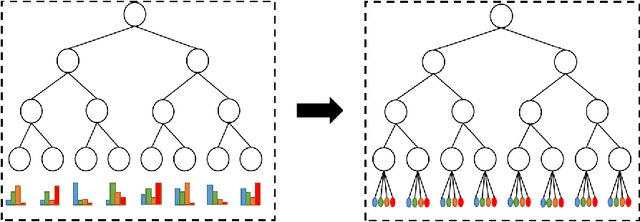
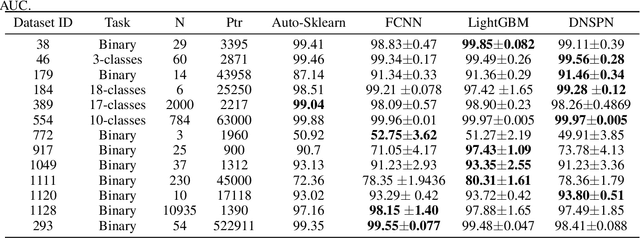
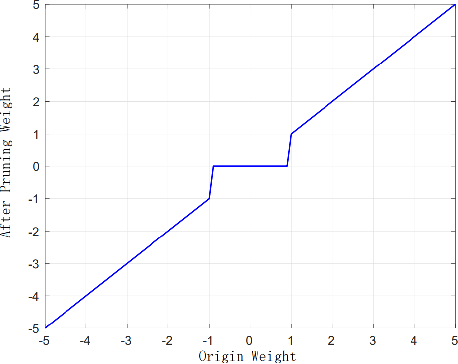
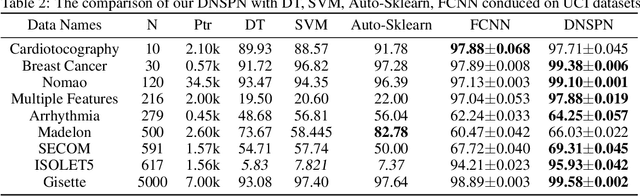
To deal with datasets of different complexity, this paper presents an efficient learning model that combines the proposed Dynamic Connected Neural Decision Networks (DNDN) and a new pruning method--Dynamic Soft Pruning (DSP). DNDN is a combination of random forests and deep neural networks thereby it enjoys both the properties of powerful classification capability and representation learning functionality. Different from Deep Neural Decision Forests (DNDF), this paper adopts an end-to-end training approach by representing the classification distribution with multiple randomly initialized softmax layers, which enables the placement of the forest trees after each layer in the neural network and greatly improves the training speed and stability. Furthermore, DSP is proposed to reduce the redundant connections of the network in a soft fashion which has high flexibility but demonstrates no performance loss compared with previous approaches. Extensive experiments on different datasets demonstrate the superiority of the proposed model over other popular algorithms in solving classification tasks.

Regression via Arbitrary Quantile Modeling

In the regression problem, L1 and L2 are the most commonly used loss functions, which produce mean predictions with different biases. However, the predictions are neither robust nor adequate enough since they only capture a few conditional distributions instead of the whole distribution, especially for small datasets. To address this problem, we proposed arbitrary quantile modeling to regulate the prediction, which achieved better performance compared to traditional loss functions. More specifically, a new distribution regression method, Deep Distribution Regression (DDR), is proposed to estimate arbitrary quantiles of the response variable. Our DDR method consists of two models: a Q model, which predicts the corresponding value for arbitrary quantile, and an F model, which predicts the corresponding quantile for arbitrary value. Furthermore, the duality between Q and F models enables us to design a novel loss function for joint training and perform a dual inference mechanism. Our experiments demonstrate that our DDR-joint and DDR-disjoint methods outperform previous methods such as AdaBoost, random forest, LightGBM, and neural networks both in terms of mean and quantile prediction.

Short-and-Sparse Deconvolution -- A Geometric Approach

Short-and-sparse deconvolution (SaSD) is the problem of extracting localized, recurring motifs in signals with spatial or temporal structure. Variants of this problem arise in applications such as image deblurring, microscopy, neural spike sorting, and more. The problem is challenging in both theory and practice, as natural optimization formulations are nonconvex. Moreover, practical deconvolution problems involve smooth motifs (kernels) whose spectra decay rapidly, resulting in poor conditioning and numerical challenges. This paper is motivated by recent theoretical advances, which characterize the optimization landscape of a particular nonconvex formulation of SaSD. This is used to derive a $provable$ algorithm which exactly solves certain non-practical instances of the SaSD problem. We leverage the key ideas from this theory (sphere constraints, data-driven initialization) to develop a $practical$ algorithm, which performs well on data arising from a range of application areas. We highlight key additional challenges posed by the ill-conditioning of real SaSD problems, and suggest heuristics (acceleration, continuation, reweighting) to mitigate them. Experiments demonstrate both the performance and generality of the proposed method.

Penalized matrix decomposition for denoising, compression, and improved demixing of functional imaging data

Calcium imaging has revolutionized systems neuroscience, providing the ability to image large neural populations with single-cell resolution. The resulting datasets are quite large, which has presented a barrier to routine open sharing of this data, slowing progress in reproducible research. State of the art methods for analyzing this data are based on non-negative matrix factorization (NMF); these approaches solve a non-convex optimization problem, and are effective when good initializations are available, but can break down in low-SNR settings where common initialization approaches fail. Here we introduce an approach to compressing and denoising functional imaging data. The method is based on a spatially-localized penalized matrix decomposition (PMD) of the data to separate (low-dimensional) signal from (temporally-uncorrelated) noise. This approach can be applied in parallel on local spatial patches and is therefore highly scalable, does not impose non-negativity constraints or require stringent identifiability assumptions (leading to significantly more robust results compared to NMF), and estimates all parameters directly from the data, so no hand-tuning is required. We have applied the method to a wide range of functional imaging data (including one-photon, two-photon, three-photon, widefield, somatic, axonal, dendritic, calcium, and voltage imaging datasets): in all cases, we observe ~2-4x increases in SNR and compression rates of 20-300x with minimal visible loss of signal, with no adjustment of hyperparameters; this in turn facilitates the process of demixing the observed activity into contributions from individual neurons. We focus on two challenging applications: dendritic calcium imaging data and voltage imaging data in the context of optogenetic stimulation. In both cases, we show that our new approach leads to faster and much more robust extraction of activity from the data.