Boosting Semi-Supervised Medical Image Segmentation via Masked Image Consistency and Discrepancy Learning

Semi-supervised learning is of great significance in medical image segmentation by exploiting unlabeled data. Among its strategies, the co-training framework is prominent. However, previous co-training studies predominantly concentrate on network initialization variances and pseudo-label generation, while overlooking the equilibrium between information interchange and model diversity preservation. In this paper, we propose the Masked Image Consistency and Discrepancy Learning (MICD) framework with three key modules. The Masked Cross Pseudo Consistency (MCPC) module enriches context perception and small sample learning via pseudo-labeling across masked-input branches. The Cross Feature Consistency (CFC) module fortifies information exchange and model robustness by ensuring decoder feature consistency. The Cross Model Discrepancy (CMD) module utilizes EMA teacher networks to oversee outputs and preserve branch diversity. Together, these modules address existing limitations by focusing on fine-grained local information and maintaining diversity in a heterogeneous framework. Experiments on two public medical image datasets, AMOS and Synapse, demonstrate that our approach outperforms state-of-the-art methods.

Asymptotically Efficient Online Learning for Censored Regression Models Under Non-I.I.D Data

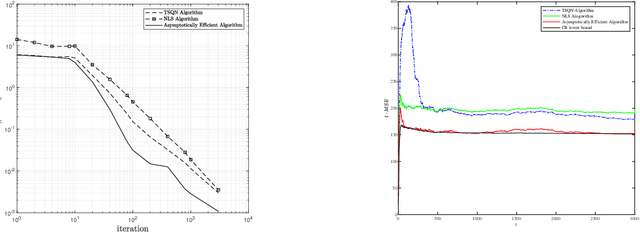
The asymptotically efficient online learning problem is investigated for stochastic censored regression models, which arise from various fields of learning and statistics but up to now still lacks comprehensive theoretical studies on the efficiency of the learning algorithms. For this, we propose a two-step online algorithm, where the first step focuses on achieving algorithm convergence, and the second step is dedicated to improving the estimation performance. Under a general excitation condition on the data, we show that our algorithm is strongly consistent and asymptotically normal by employing the stochastic Lyapunov function method and limit theories for martingales. Moreover, we show that the covariances of the estimates can achieve the Cramer-Rao (C-R) bound asymptotically, indicating that the performance of the proposed algorithm is the best possible that one can expect in general. Unlike most of the existing works, our results are obtained without resorting to the traditionally used but stringent conditions such as independent and identically distributed (i.i.d) assumption on the data, and thus our results do not exclude applications to stochastic dynamical systems with feedback. A numerical example is also provided to illustrate the superiority of the proposed online algorithm over the existing related ones in the literature.

A Two-Step Quasi-Newton Identification Algorithm for Stochastic Systems with Saturated Observations

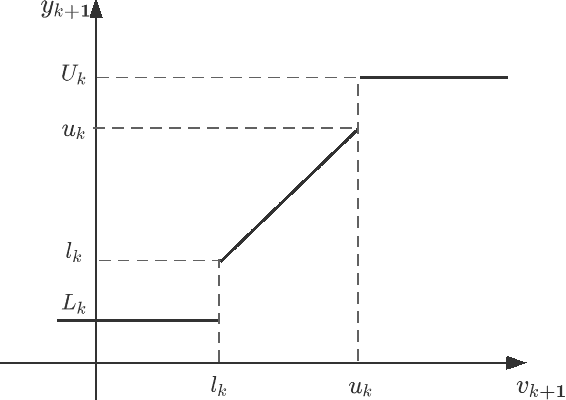
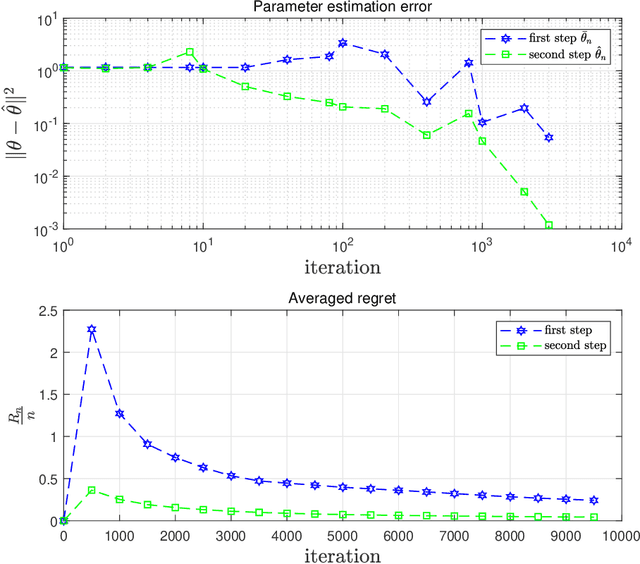
This paper investigates the identification and prediction problems for stochastic dynamical systems with saturated observations, which arise from various fields in engineering and social systems, but still lack comprehensive theoretical studies up to now. The main contributions of this paper are: (i) To introduce a two-step Quasi-Newton (TSQN) identification algorithm which is applicable to a typical class of nonlinear stochastic systems with outputs observed under possibly varying saturations. (ii) To establish the convergence of both the parameter estimators and adaptive predictors and to prove the asymptotic normality, under a weakest possible non-persistent excitation (PE) condition, which can be applied to stochastic feedback systems with general non-stationary and correlated system signals or data. (iii) To establish probabilistic estimation error bounds for any given finite number of data, by using either martingale inequalities or Monte Carlo experiments. A numerical example is also provided to illustrated the performance of our identification algorithm.

A Histopathology Study Comparing Contrastive Semi-Supervised and Fully Supervised Learning

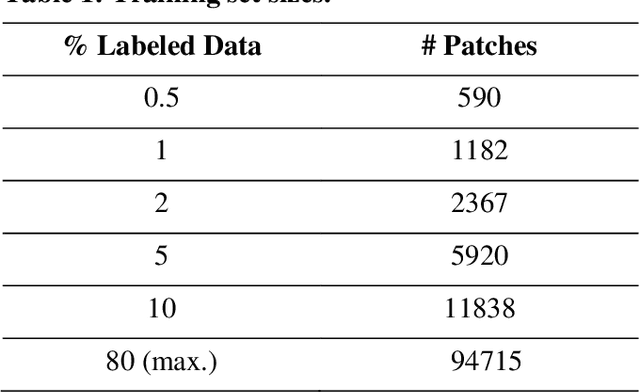
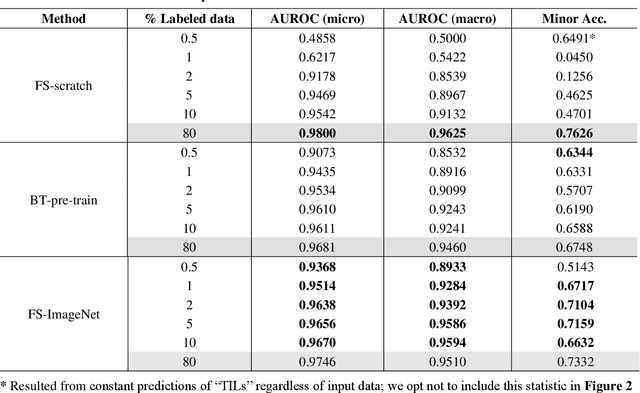
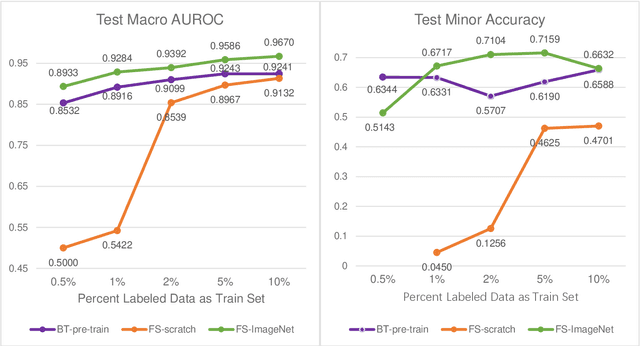
Data labeling is often the most challenging task when developing computational pathology models. Pathologist participation is necessary to generate accurate labels, and the limitations on pathologist time and demand for large, labeled datasets has led to research in areas including weakly supervised learning using patient-level labels, machine assisted annotation and active learning. In this paper we explore self-supervised learning to reduce labeling burdens in computational pathology. We explore this in the context of classification of breast cancer tissue using the Barlow Twins approach, and we compare self-supervision with alternatives like pre-trained networks in low-data scenarios. For the task explored in this paper, we find that ImageNet pre-trained networks largely outperform the self-supervised representations obtained using Barlow Twins.

Identification and Adaptation with Binary-Valued Observations under Non-Persistent Excitation Condition

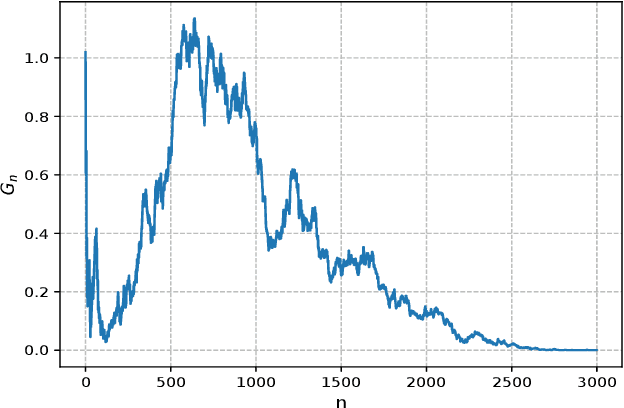
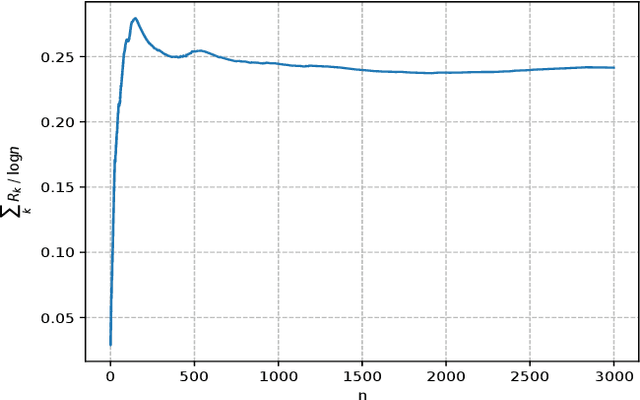
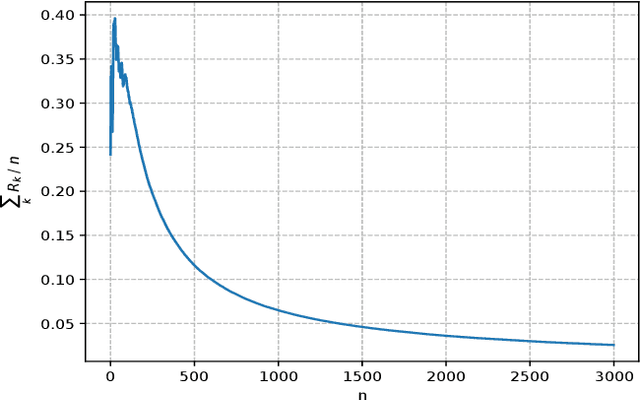
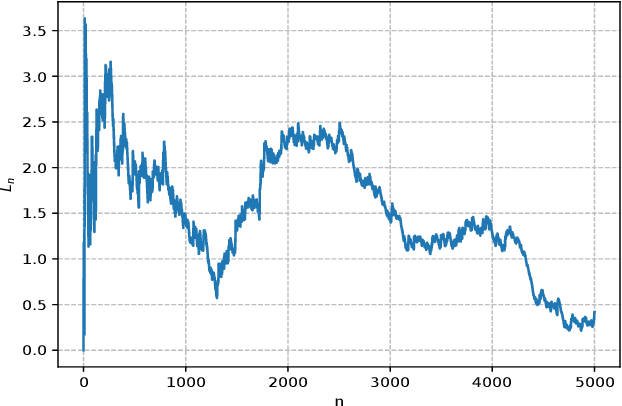
Dynamical systems with binary-valued observations are widely used in information industry, technology of biological pharmacy and other fields. Though there have been much efforts devoted to the identification of such systems, most of the previous investigations are based on first-order gradient algorithm which usually has much slower convergence rate than the Quasi-Newton algorithm. Moreover, persistence of excitation(PE) conditions are usually required to guarantee consistent parameter estimates in the existing literature, which are hard to be verified or guaranteed for feedback control systems. In this paper, we propose an online projected Quasi-Newton type algorithm for parameter estimation of stochastic regression models with binary-valued observations and varying thresholds. By using both the stochastic Lyapunov function and martingale estimation methods, we establish the strong consistency of the estimation algorithm and provide the convergence rate, under a signal condition which is considerably weaker than the traditional PE condition and coincides with the weakest possible excitation known for the classical least square algorithm of stochastic regression models. Convergence of adaptive predictors and their applications in adaptive control are also discussed.