Consensus-Based Distributed Nonlinear Filtering with Kernel Mean Embedding

This paper proposes a consensus-based distributed nonlinear filter with kernel mean embedding (KME). This fills with gap of posterior density approximation with KME for distributed nonlinear dynamic systems. To approximate the posterior density, the system state is embedded into a higher-dimensional reproducing kernel Hilbert space (RKHS), and then the nonlinear measurement function is linearly converted. As a result, an update rule of KME of posterior distribution is established in the RKHS. To show the proposed distributed filter being capable of achieving the centralized estimation accuracy, a centralized filter, serving as an extension of the standard Kalman filter in the state space to the RKHS, is developed first. Benefited from the KME, the proposed distributed filter converges to the centralized one while maintaining the distributed pattern. Two examples are introduced to demonstrate the effectiveness of the developed filters in target tracking scenarios including nearly constantly moving target and turning target, respectively, with bearing-only, range and bearing measurements.

Identification and Adaptation with Binary-Valued Observations under Non-Persistent Excitation Condition

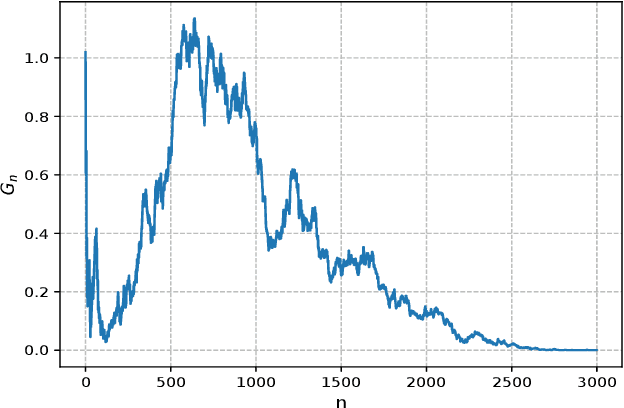
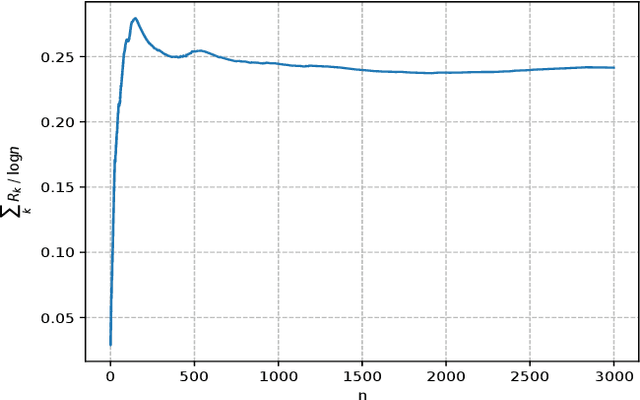
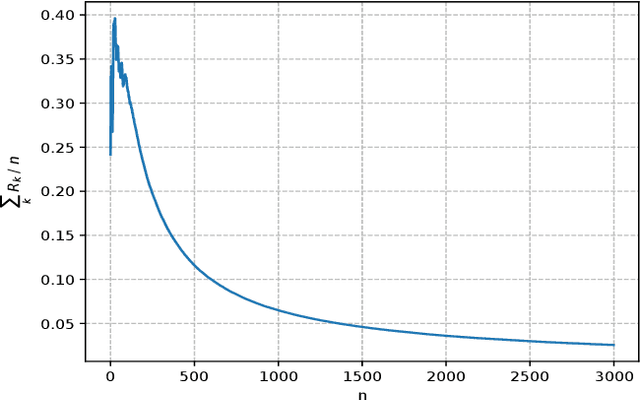
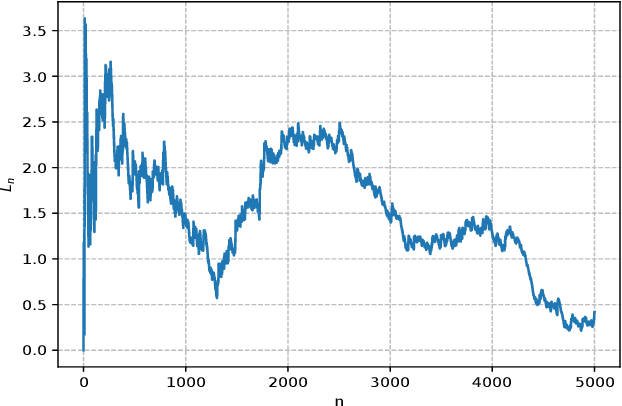
Dynamical systems with binary-valued observations are widely used in information industry, technology of biological pharmacy and other fields. Though there have been much efforts devoted to the identification of such systems, most of the previous investigations are based on first-order gradient algorithm which usually has much slower convergence rate than the Quasi-Newton algorithm. Moreover, persistence of excitation(PE) conditions are usually required to guarantee consistent parameter estimates in the existing literature, which are hard to be verified or guaranteed for feedback control systems. In this paper, we propose an online projected Quasi-Newton type algorithm for parameter estimation of stochastic regression models with binary-valued observations and varying thresholds. By using both the stochastic Lyapunov function and martingale estimation methods, we establish the strong consistency of the estimation algorithm and provide the convergence rate, under a signal condition which is considerably weaker than the traditional PE condition and coincides with the weakest possible excitation known for the classical least square algorithm of stochastic regression models. Convergence of adaptive predictors and their applications in adaptive control are also discussed.