A Two-Step Quasi-Newton Identification Algorithm for Stochastic Systems with Saturated Observations

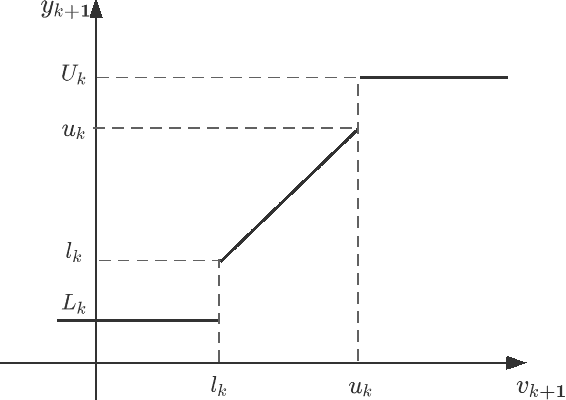
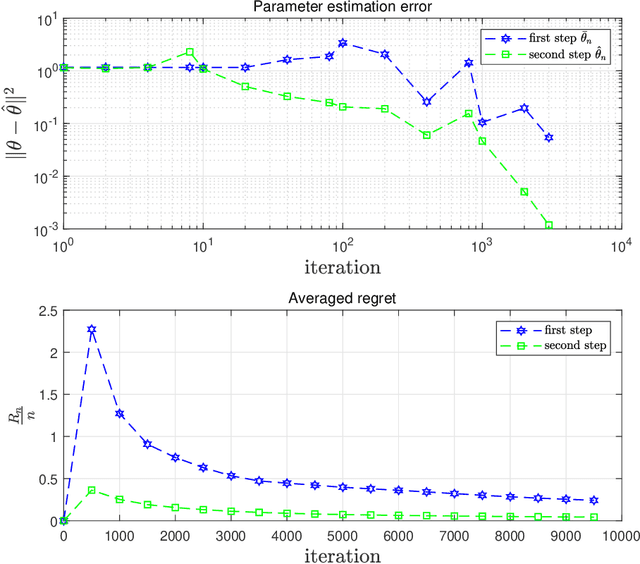
This paper investigates the identification and prediction problems for stochastic dynamical systems with saturated observations, which arise from various fields in engineering and social systems, but still lack comprehensive theoretical studies up to now. The main contributions of this paper are: (i) To introduce a two-step Quasi-Newton (TSQN) identification algorithm which is applicable to a typical class of nonlinear stochastic systems with outputs observed under possibly varying saturations. (ii) To establish the convergence of both the parameter estimators and adaptive predictors and to prove the asymptotic normality, under a weakest possible non-persistent excitation (PE) condition, which can be applied to stochastic feedback systems with general non-stationary and correlated system signals or data. (iii) To establish probabilistic estimation error bounds for any given finite number of data, by using either martingale inequalities or Monte Carlo experiments. A numerical example is also provided to illustrated the performance of our identification algorithm.