Asymptotically Efficient Online Learning for Censored Regression Models Under Non-I.I.D Data
Paper and Code
Oct 01, 2023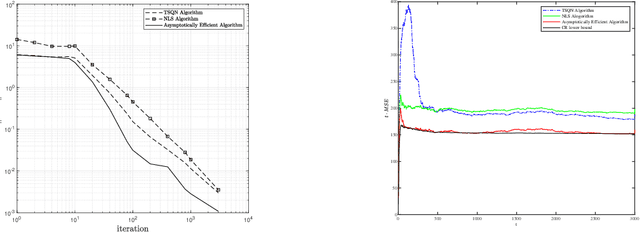
The asymptotically efficient online learning problem is investigated for stochastic censored regression models, which arise from various fields of learning and statistics but up to now still lacks comprehensive theoretical studies on the efficiency of the learning algorithms. For this, we propose a two-step online algorithm, where the first step focuses on achieving algorithm convergence, and the second step is dedicated to improving the estimation performance. Under a general excitation condition on the data, we show that our algorithm is strongly consistent and asymptotically normal by employing the stochastic Lyapunov function method and limit theories for martingales. Moreover, we show that the covariances of the estimates can achieve the Cramer-Rao (C-R) bound asymptotically, indicating that the performance of the proposed algorithm is the best possible that one can expect in general. Unlike most of the existing works, our results are obtained without resorting to the traditionally used but stringent conditions such as independent and identically distributed (i.i.d) assumption on the data, and thus our results do not exclude applications to stochastic dynamical systems with feedback. A numerical example is also provided to illustrate the superiority of the proposed online algorithm over the existing related ones in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge