Short-and-Sparse Deconvolution -- A Geometric Approach

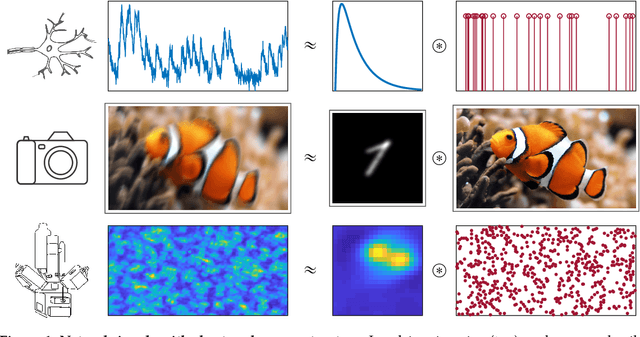
Short-and-sparse deconvolution (SaSD) is the problem of extracting localized, recurring motifs in signals with spatial or temporal structure. Variants of this problem arise in applications such as image deblurring, microscopy, neural spike sorting, and more. The problem is challenging in both theory and practice, as natural optimization formulations are nonconvex. Moreover, practical deconvolution problems involve smooth motifs (kernels) whose spectra decay rapidly, resulting in poor conditioning and numerical challenges. This paper is motivated by recent theoretical advances, which characterize the optimization landscape of a particular nonconvex formulation of SaSD. This is used to derive a $provable$ algorithm which exactly solves certain non-practical instances of the SaSD problem. We leverage the key ideas from this theory (sphere constraints, data-driven initialization) to develop a $practical$ algorithm, which performs well on data arising from a range of application areas. We highlight key additional challenges posed by the ill-conditioning of real SaSD problems, and suggest heuristics (acceleration, continuation, reweighting) to mitigate them. Experiments demonstrate both the performance and generality of the proposed method.

Compressed Sensing Microscopy with Scanning Line Probes

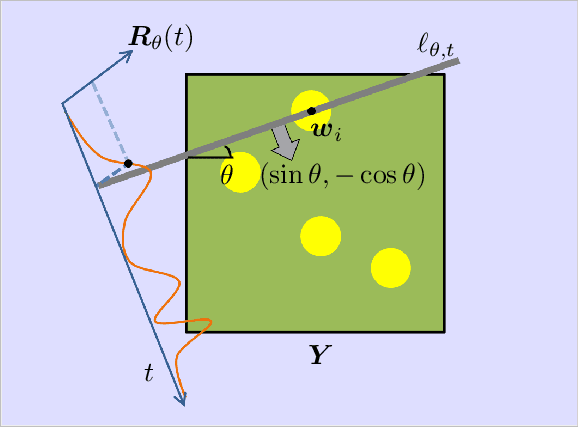
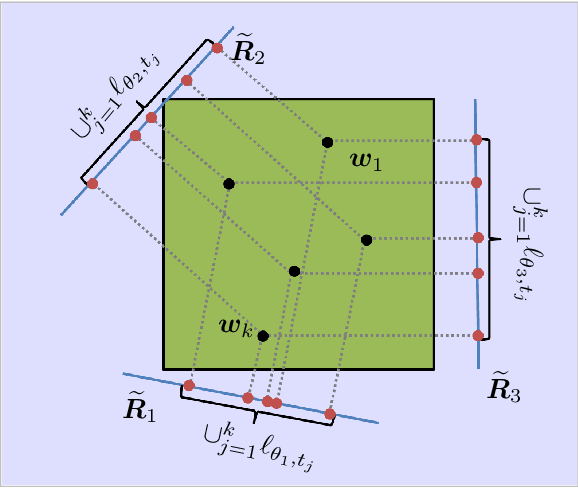
In applications of scanning probe microscopy, images are acquired by raster scanning a point probe across a sample. Viewed from the perspective of compressed sensing (CS), this pointwise sampling scheme is inefficient, especially when the target image is structured. While replacing point measurements with delocalized, incoherent measurements has the potential to yield order-of-magnitude improvements in scan time, implementing the delocalized measurements of CS theory is challenging. In this paper we study a partially delocalized probe construction, in which the point probe is replaced with a continuous line, creating a sensor which essentially acquires line integrals of the target image. We show through simulations, rudimentary theoretical analysis, and experiments, that these line measurements can image sparse samples far more efficiently than traditional point measurements, provided the local features in the sample are enough separated. Despite this promise, practical reconstruction from line measurements poses additional difficulties: the measurements are partially coherent, and real measurements exhibit nonidealities. We show how to overcome these limitations using natural strategies (reweighting to cope with coherence, blind calibration for nonidealities), culminating in an end-to-end demonstration.

On the Global Geometry of Sphere-Constrained Sparse Blind Deconvolution

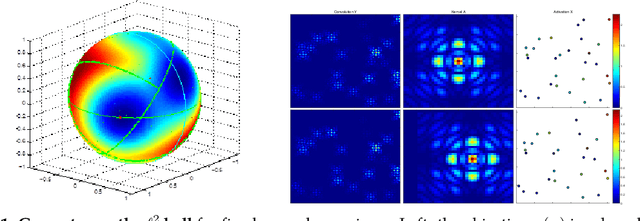
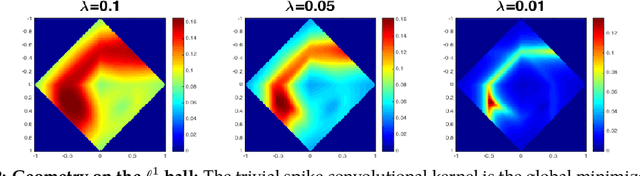
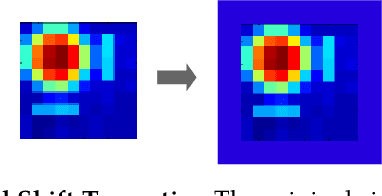
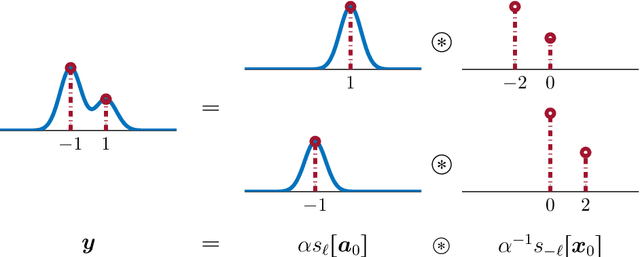
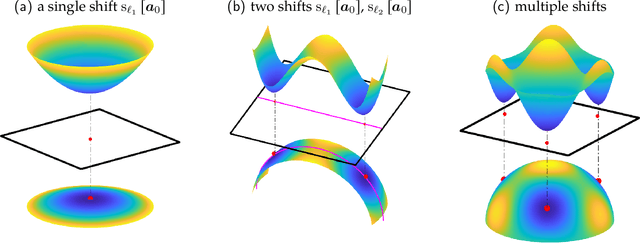
Blind deconvolution is the problem of recovering a convolutional kernel $\boldsymbol a_0$ and an activation signal $\boldsymbol x_0$ from their convolution $\boldsymbol y = \boldsymbol a_0 \circledast \boldsymbol x_0$. This problem is ill-posed without further constraints or priors. This paper studies the situation where the nonzero entries in the activation signal are sparsely and randomly populated. We normalize the convolution kernel to have unit Frobenius norm and cast the sparse blind deconvolution problem as a nonconvex optimization problem over the sphere. With this spherical constraint, every spurious local minimum turns out to be close to some signed shift truncation of the ground truth, under certain hypotheses. This benign property motivates an effective two stage algorithm that recovers the ground truth from the partial information offered by a suboptimal local minimum. This geometry-inspired algorithm recovers the ground truth for certain microscopy problems, also exhibits promising performance in the more challenging image deblurring problem. Our insights into the global geometry and the two stage algorithm extend to the convolutional dictionary learning problem, where a superposition of multiple convolution signals is observed.

Geometry and Symmetry in Short-and-Sparse Deconvolution

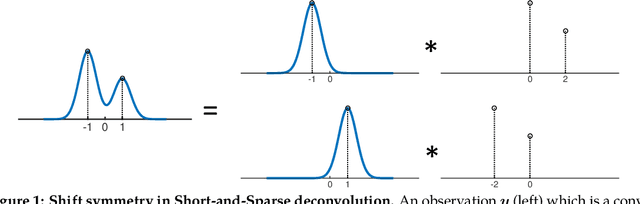
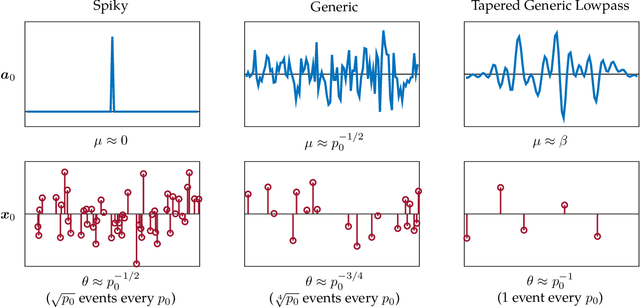
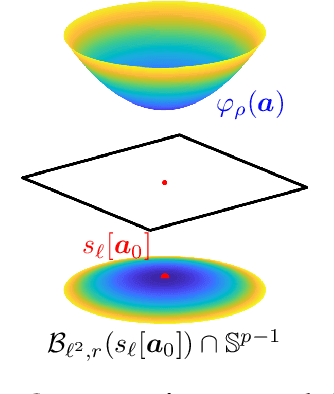
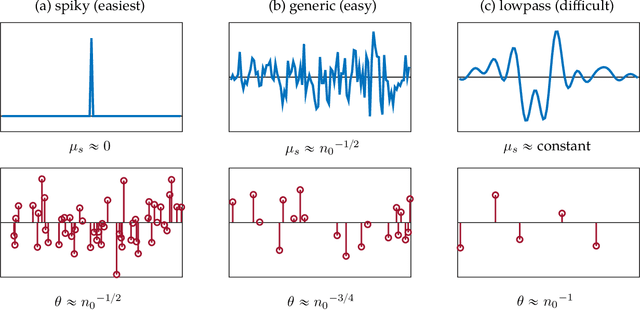
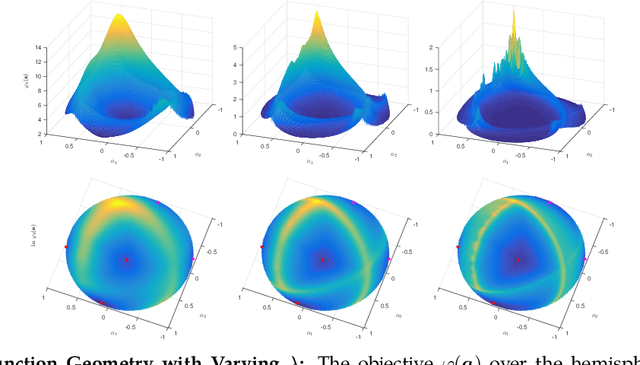
We study the $\textit{Short-and-Sparse (SaS) deconvolution}$ problem of recovering a short signal $\mathbf a_0$ and a sparse signal $\mathbf x_0$ from their convolution. We propose a method based on nonconvex optimization, which under certain conditions recovers the target short and sparse signals, up to a signed shift symmetry which is intrinsic to this model. This symmetry plays a central role in shaping the optimization landscape for deconvolution. We give a $\textit{regional analysis}$, which characterizes this landscape geometrically, on a union of subspaces. Our geometric characterization holds when the length-$p_0$ short signal $\mathbf a_0$ has shift coherence $\mu$, and $\mathbf x_0$ follows a random sparsity model with sparsity rate $\theta \in \Bigl[\frac{c_1}{p_0}, \frac{c_2}{p_0\sqrt\mu + \sqrt{p_0}}\Bigr]\cdot\frac{1}{\log^2p_0}$. Based on this geometry, we give a provable method that successfully solves SaS deconvolution with high probability.

Structured Local Optima in Sparse Blind Deconvolution

Blind deconvolution is a ubiquitous problem of recovering two unknown signals from their convolution. Unfortunately, this is an ill-posed problem in general. This paper focuses on the {\em short and sparse} blind deconvolution problem, where the one unknown signal is short and the other one is sparsely and randomly supported. This variant captures the structure of the unknown signals in several important applications. We assume the short signal to have unit $\ell^2$ norm and cast the blind deconvolution problem as a nonconvex optimization problem over the sphere. We demonstrate that (i) in a certain region of the sphere, every local optimum is close to some shift truncation of the ground truth, and (ii) for a generic short signal of length $k$, when the sparsity of activation signal $\theta\lesssim k^{-2/3}$ and number of measurements $m\gtrsim poly(k)$, a simple initialization method together with a descent algorithm which escapes strict saddle points recovers a near shift truncation of the ground truth kernel.