Geometry and Symmetry in Short-and-Sparse Deconvolution
Paper and Code
Jan 02, 2019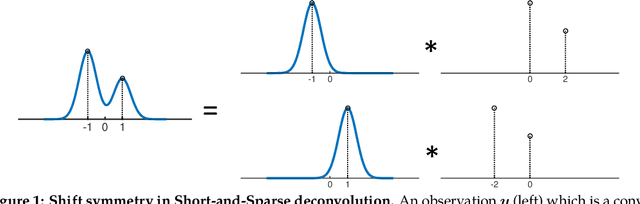
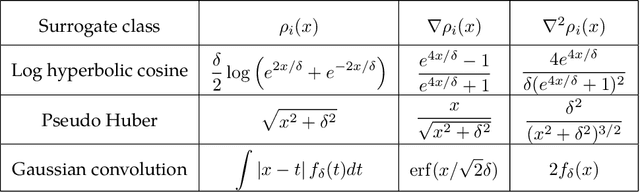
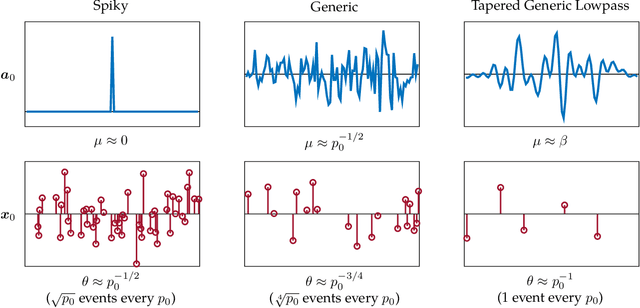
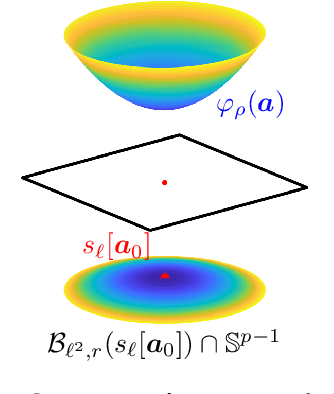
We study the $\textit{Short-and-Sparse (SaS) deconvolution}$ problem of recovering a short signal $\mathbf a_0$ and a sparse signal $\mathbf x_0$ from their convolution. We propose a method based on nonconvex optimization, which under certain conditions recovers the target short and sparse signals, up to a signed shift symmetry which is intrinsic to this model. This symmetry plays a central role in shaping the optimization landscape for deconvolution. We give a $\textit{regional analysis}$, which characterizes this landscape geometrically, on a union of subspaces. Our geometric characterization holds when the length-$p_0$ short signal $\mathbf a_0$ has shift coherence $\mu$, and $\mathbf x_0$ follows a random sparsity model with sparsity rate $\theta \in \Bigl[\frac{c_1}{p_0}, \frac{c_2}{p_0\sqrt\mu + \sqrt{p_0}}\Bigr]\cdot\frac{1}{\log^2p_0}$. Based on this geometry, we give a provable method that successfully solves SaS deconvolution with high probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge