PRISM: A hierarchical multiscale approach for time series forecasting

Forecasting is critical in areas such as finance, biology, and healthcare. Despite the progress in the field, making accurate forecasts remains challenging because real-world time series contain both global trends, local fine-grained structure, and features on multiple scales in between. Here, we present a new forecasting method, PRISM (Partitioned Representation for Iterative Sequence Modeling), that addresses this challenge through a learnable tree-based partitioning of the signal. At the root of the tree, a global representation captures coarse trends in the signal, while recursive splits reveal increasingly localized views of the signal. At each level of the tree, data are projected onto a time-frequency basis (e.g., wavelets or exponential moving averages) to extract scale-specific features, which are then aggregated across the hierarchy. This design allows the model to jointly capture global structure and local dynamics of the signal, enabling accurate forecasting. Experiments across benchmark datasets show that our method outperforms state-of-the-art methods for forecasting. Overall, these results demonstrate that our hierarchical approach provides a lightweight and flexible framework for forecasting multivariate time series. The code is available at https://github.com/nerdslab/prism.

Neural Encoding and Decoding at Scale

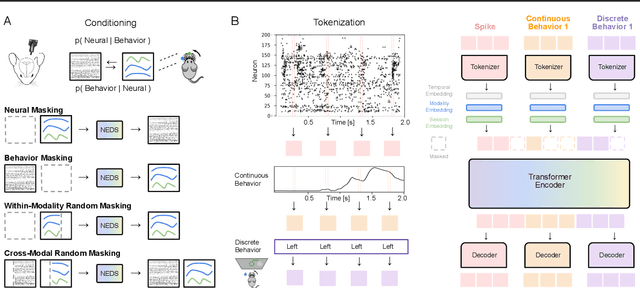
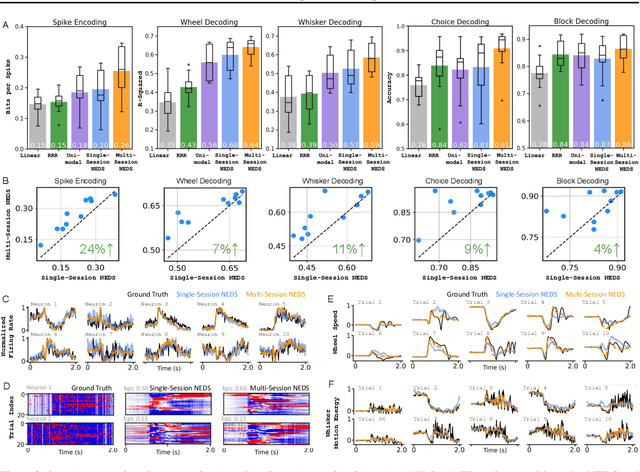
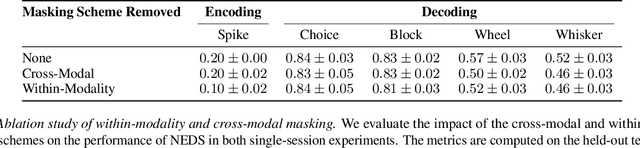
Recent work has demonstrated that large-scale, multi-animal models are powerful tools for characterizing the relationship between neural activity and behavior. Current large-scale approaches, however, focus exclusively on either predicting neural activity from behavior (encoding) or predicting behavior from neural activity (decoding), limiting their ability to capture the bidirectional relationship between neural activity and behavior. To bridge this gap, we introduce a multimodal, multi-task model that enables simultaneous Neural Encoding and Decoding at Scale (NEDS). Central to our approach is a novel multi-task-masking strategy, which alternates between neural, behavioral, within-modality, and cross-modality masking. We pretrain our method on the International Brain Laboratory (IBL) repeated site dataset, which includes recordings from 83 animals performing the same visual decision-making task. In comparison to other large-scale models, we demonstrate that NEDS achieves state-of-the-art performance for both encoding and decoding when pretrained on multi-animal data and then fine-tuned on new animals. Surprisingly, NEDS's learned embeddings exhibit emergent properties: even without explicit training, they are highly predictive of the brain regions in each recording. Altogether, our approach is a step towards a foundation model of the brain that enables seamless translation between neural activity and behavior.

Towards a "universal translator" for neural dynamics at single-cell, single-spike resolution

Neuroscience research has made immense progress over the last decade, but our understanding of the brain remains fragmented and piecemeal: the dream of probing an arbitrary brain region and automatically reading out the information encoded in its neural activity remains out of reach. In this work, we build towards a first foundation model for neural spiking data that can solve a diverse set of tasks across multiple brain areas. We introduce a novel self-supervised modeling approach for population activity in which the model alternates between masking out and reconstructing neural activity across different time steps, neurons, and brain regions. To evaluate our approach, we design unsupervised and supervised prediction tasks using the International Brain Laboratory repeated site dataset, which is comprised of Neuropixels recordings targeting the same brain locations across 48 animals and experimental sessions. The prediction tasks include single-neuron and region-level activity prediction, forward prediction, and behavior decoding. We demonstrate that our multi-task-masking (MtM) approach significantly improves the performance of current state-of-the-art population models and enables multi-task learning. We also show that by training on multiple animals, we can improve the generalization ability of the model to unseen animals, paving the way for a foundation model of the brain at single-cell, single-spike resolution.

GraphFM: A Scalable Framework for Multi-Graph Pretraining

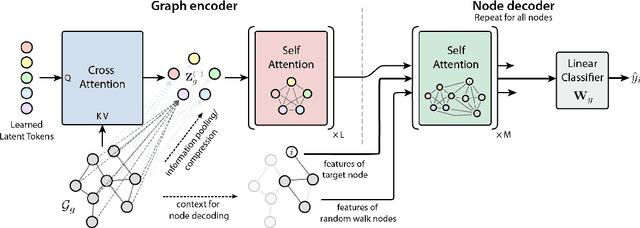
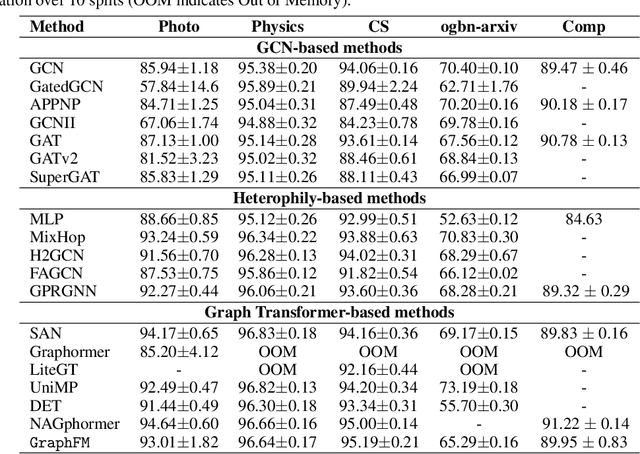
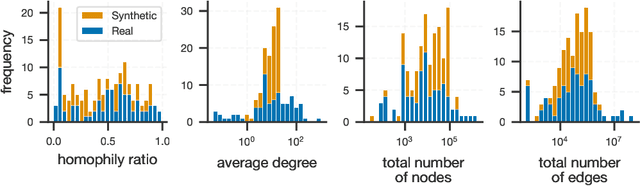
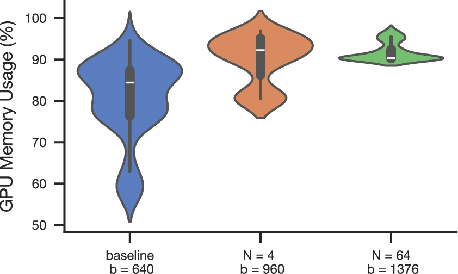
Graph neural networks are typically trained on individual datasets, often requiring highly specialized models and extensive hyperparameter tuning. This dataset-specific approach arises because each graph dataset often has unique node features and diverse connectivity structures, making it difficult to build a generalist model. To address these challenges, we introduce a scalable multi-graph multi-task pretraining approach specifically tailored for node classification tasks across diverse graph datasets from different domains. Our method, Graph Foundation Model (GraphFM), leverages a Perceiver-based encoder that employs learned latent tokens to compress domain-specific features into a common latent space. This approach enhances the model's ability to generalize across different graphs and allows for scaling across diverse data. We demonstrate the efficacy of our approach by training a model on 152 different graph datasets comprising over 7.4 million nodes and 189 million edges, establishing the first set of scaling laws for multi-graph pretraining on datasets spanning many domains (e.g., molecules, citation and product graphs). Our results show that pretraining on a diverse array of real and synthetic graphs improves the model's adaptability and stability, while performing competitively with state-of-the-art specialist models. This work illustrates that multi-graph pretraining can significantly reduce the burden imposed by the current graph training paradigm, unlocking new capabilities for the field of graph neural networks by creating a single generalist model that performs competitively across a wide range of datasets and tasks.

Convex Relaxation Regression: Black-Box Optimization of Smooth Functions by Learning Their Convex Envelopes

Finding efficient and provable methods to solve non-convex optimization problems is an outstanding challenge in machine learning and optimization theory. A popular approach used to tackle non-convex problems is to use convex relaxation techniques to find a convex surrogate for the problem. Unfortunately, convex relaxations typically must be found on a problem-by-problem basis. Thus, providing a general-purpose strategy to estimate a convex relaxation would have a wide reaching impact. Here, we introduce Convex Relaxation Regression (CoRR), an approach for learning convex relaxations for a class of smooth functions. The main idea behind our approach is to estimate the convex envelope of a function $f$ by evaluating $f$ at a set of $T$ random points and then fitting a convex function to these function evaluations. We prove that with probability greater than $1-\delta$, the solution of our algorithm converges to the global optimizer of $f$ with error $\mathcal{O} \Big( \big(\frac{\log(1/\delta) }{T} \big)^{\alpha} \Big)$ for some $\alpha> 0$. Our approach enables the use of convex optimization tools to solve a class of non-convex optimization problems.