Extremely Greedy Equivalence Search

The goal of causal discovery is to learn a directed acyclic graph from data. One of the most well-known methods for this problem is Greedy Equivalence Search (GES). GES searches for the graph by incrementally and greedily adding or removing edges to maximize a model selection criterion. It has strong theoretical guarantees on infinite data but can fail in practice on finite data. In this paper, we first identify some of the causes of GES's failure, finding that it can get blocked in local optima, especially in denser graphs. We then propose eXtremely Greedy Equivalent Search (XGES), which involves a new heuristic to improve the search strategy of GES while retaining its theoretical guarantees. In particular, XGES favors deleting edges early in the search over inserting edges, which reduces the possibility of the search ending in local optima. A further contribution of this work is an efficient algorithmic formulation of XGES (and GES). We benchmark XGES on simulated datasets with known ground truth. We find that XGES consistently outperforms GES in recovering the correct graphs, and it is 10 times faster. XGES implementations in Python and C++ are available at https://github.com/ANazaret/XGES.

Posterior Mean Matching: Generative Modeling through Online Bayesian Inference

This paper introduces posterior mean matching (PMM), a new method for generative modeling that is grounded in Bayesian inference. PMM uses conjugate pairs of distributions to model complex data of various modalities like images and text, offering a flexible alternative to existing methods like diffusion models. PMM models iteratively refine noisy approximations of the target distribution using updates from online Bayesian inference. PMM is flexible because its mechanics are based on general Bayesian models. We demonstrate this flexibility by developing specialized examples: a generative PMM model of real-valued data using the Normal-Normal model, a generative PMM model of count data using a Gamma-Poisson model, and a generative PMM model of discrete data using a Dirichlet-Categorical model. For the Normal-Normal PMM model, we establish a direct connection to diffusion models by showing that its continuous-time formulation converges to a stochastic differential equation (SDE). Additionally, for the Gamma-Poisson PMM, we derive a novel SDE driven by a Cox process, which is a significant departure from traditional Brownian motion-based generative models. PMMs achieve performance that is competitive with generative models for language modeling and image generation.

Can Generative AI Solve Your In-Context Learning Problem? A Martingale Perspective

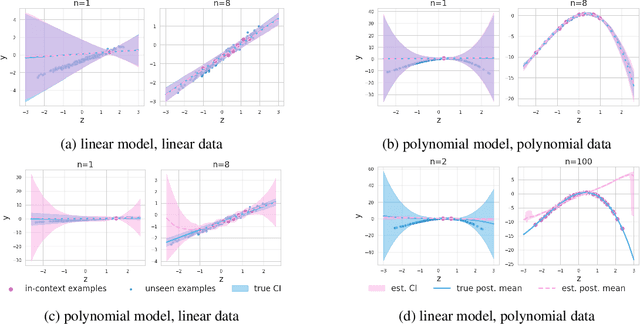
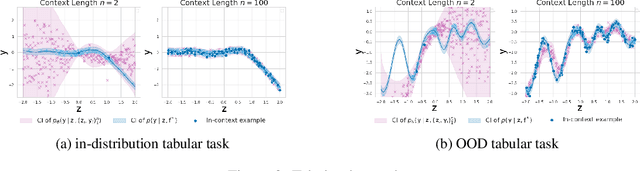
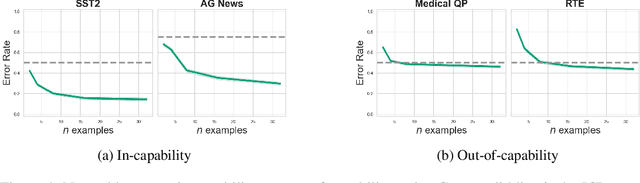
This work is about estimating when a conditional generative model (CGM) can solve an in-context learning (ICL) problem. An in-context learning (ICL) problem comprises a CGM, a dataset, and a prediction task. The CGM could be a multi-modal foundation model; the dataset, a collection of patient histories, test results, and recorded diagnoses; and the prediction task to communicate a diagnosis to a new patient. A Bayesian interpretation of ICL assumes that the CGM computes a posterior predictive distribution over an unknown Bayesian model defining a joint distribution over latent explanations and observable data. From this perspective, Bayesian model criticism is a reasonable approach to assess the suitability of a given CGM for an ICL problem. However, such approaches -- like posterior predictive checks (PPCs) -- often assume that we can sample from the likelihood and posterior defined by the Bayesian model, which are not explicitly given for contemporary CGMs. To address this, we show when ancestral sampling from the predictive distribution of a CGM is equivalent to sampling datasets from the posterior predictive of the assumed Bayesian model. Then we develop the generative predictive $p$-value, which enables PPCs and their cousins for contemporary CGMs. The generative predictive $p$-value can then be used in a statistical decision procedure to determine when the model is appropriate for an ICL problem. Our method only requires generating queries and responses from a CGM and evaluating its response log probability. We empirically evaluate our method on synthetic tabular, imaging, and natural language ICL tasks using large language models.

Multi-environment Topic Models

Probabilistic topic models are a powerful tool for extracting latent themes from large text datasets. In many text datasets, we also observe per-document covariates (e.g., source, style, political affiliation) that act as environments that modulate a "global" (environment-agnostic) topic representation. Accurately learning these representations is important for prediction on new documents in unseen environments and for estimating the causal effect of topics on real-world outcomes. To this end, we introduce the Multi-environment Topic Model (MTM), an unsupervised probabilistic model that separates global and environment-specific terms. Through experimentation on various political content, from ads to tweets and speeches, we show that the MTM produces interpretable global topics with distinct environment-specific words. On multi-environment data, the MTM outperforms strong baselines in and out-of-distribution. It also enables the discovery of accurate causal effects.

Treeffuser: Probabilistic Predictions via Conditional Diffusions with Gradient-Boosted Trees

Probabilistic prediction aims to compute predictive distributions rather than single-point predictions. These distributions enable practitioners to quantify uncertainty, compute risk, and detect outliers. However, most probabilistic methods assume parametric responses, such as Gaussian or Poisson distributions. When these assumptions fail, such models lead to bad predictions and poorly calibrated uncertainty. In this paper, we propose Treeffuser, an easy-to-use method for probabilistic prediction on tabular data. The idea is to learn a conditional diffusion model where the score function is estimated using gradient-boosted trees. The conditional diffusion model makes Treeffuser flexible and non-parametric, while the gradient-boosted trees make it robust and easy to train on CPUs. Treeffuser learns well-calibrated predictive distributions and can handle a wide range of regression tasks -- including those with multivariate, multimodal, and skewed responses. % , as well as categorical predictors and missing data We study Treeffuser on synthetic and real data and show that it outperforms existing methods, providing better-calibrated probabilistic predictions. We further demonstrate its versatility with an application to inventory allocation under uncertainty using sales data from Walmart. We implement Treeffuser in \href{https://github.com/blei-lab/treeffuser}{https://github.com/blei-lab/treeffuser}.

Estimating the Hallucination Rate of Generative AI

This work is about estimating the hallucination rate for in-context learning (ICL) with Generative AI. In ICL, a conditional generative model (CGM) is prompted with a dataset and asked to make a prediction based on that dataset. The Bayesian interpretation of ICL assumes that the CGM is calculating a posterior predictive distribution over an unknown Bayesian model of a latent parameter and data. With this perspective, we define a \textit{hallucination} as a generated prediction that has low-probability under the true latent parameter. We develop a new method that takes an ICL problem -- that is, a CGM, a dataset, and a prediction question -- and estimates the probability that a CGM will generate a hallucination. Our method only requires generating queries and responses from the model and evaluating its response log probability. We empirically evaluate our method on synthetic regression and natural language ICL tasks using large language models.

Extending Mean-Field Variational Inference via Entropic Regularization: Theory and Computation

Variational inference (VI) has emerged as a popular method for approximate inference for high-dimensional Bayesian models. In this paper, we propose a novel VI method that extends the naive mean field via entropic regularization, referred to as $\Xi$-variational inference ($\Xi$-VI). $\Xi$-VI has a close connection to the entropic optimal transport problem and benefits from the computationally efficient Sinkhorn algorithm. We show that $\Xi$-variational posteriors effectively recover the true posterior dependency, where the dependence is downweighted by the regularization parameter. We analyze the role of dimensionality of the parameter space on the accuracy of $\Xi$-variational approximation and how it affects computational considerations, providing a rough characterization of the statistical-computational trade-off in $\Xi$-VI. We also investigate the frequentist properties of $\Xi$-VI and establish results on consistency, asymptotic normality, high-dimensional asymptotics, and algorithmic stability. We provide sufficient criteria for achieving polynomial-time approximate inference using the method. Finally, we demonstrate the practical advantage of $\Xi$-VI over mean-field variational inference on simulated and real data.

Stable Differentiable Causal Discovery

Inferring causal relationships as directed acyclic graphs (DAGs) is an important but challenging problem. Differentiable Causal Discovery (DCD) is a promising approach to this problem, framing the search as a continuous optimization. But existing DCD methods are numerically unstable, with poor performance beyond tens of variables. In this paper, we propose Stable Differentiable Causal Discovery (SDCD), a new method that improves previous DCD methods in two ways: (1) It employs an alternative constraint for acyclicity; this constraint is more stable, both theoretically and empirically, and fast to compute. (2) It uses a training procedure tailored for sparse causal graphs, which are common in real-world scenarios. We first derive SDCD and prove its stability and correctness. We then evaluate it with both observational and interventional data and on both small-scale and large-scale settings. We find that SDCD outperforms existing methods in both convergence speed and accuracy and can scale to thousands of variables.

Causal-structure Driven Augmentations for Text OOD Generalization

The reliance of text classifiers on spurious correlations can lead to poor generalization at deployment, raising concerns about their use in safety-critical domains such as healthcare. In this work, we propose to use counterfactual data augmentation, guided by knowledge of the causal structure of the data, to simulate interventions on spurious features and to learn more robust text classifiers. We show that this strategy is appropriate in prediction problems where the label is spuriously correlated with an attribute. Under the assumptions of such problems, we discuss the favorable sample complexity of counterfactual data augmentation, compared to importance re-weighting. Pragmatically, we match examples using auxiliary data, based on diff-in-diff methodology, and use a large language model (LLM) to represent a conditional probability of text. Through extensive experimentation on learning caregiver-invariant predictors of clinical diagnoses from medical narratives and on semi-synthetic data, we demonstrate that our method for simulating interventions improves out-of-distribution (OOD) accuracy compared to baseline invariant learning algorithms.

Variational Inference with Gaussian Score Matching

Variational inference (VI) is a method to approximate the computationally intractable posterior distributions that arise in Bayesian statistics. Typically, VI fits a simple parametric distribution to the target posterior by minimizing an appropriate objective such as the evidence lower bound (ELBO). In this work, we present a new approach to VI based on the principle of score matching, that if two distributions are equal then their score functions (i.e., gradients of the log density) are equal at every point on their support. With this, we develop score matching VI, an iterative algorithm that seeks to match the scores between the variational approximation and the exact posterior. At each iteration, score matching VI solves an inner optimization, one that minimally adjusts the current variational estimate to match the scores at a newly sampled value of the latent variables. We show that when the variational family is a Gaussian, this inner optimization enjoys a closed form solution, which we call Gaussian score matching VI (GSM-VI). GSM-VI is also a ``black box'' variational algorithm in that it only requires a differentiable joint distribution, and as such it can be applied to a wide class of models. We compare GSM-VI to black box variational inference (BBVI), which has similar requirements but instead optimizes the ELBO. We study how GSM-VI behaves as a function of the problem dimensionality, the condition number of the target covariance matrix (when the target is Gaussian), and the degree of mismatch between the approximating and exact posterior distribution. We also study GSM-VI on a collection of real-world Bayesian inference problems from the posteriorDB database of datasets and models. In all of our studies we find that GSM-VI is faster than BBVI, but without sacrificing accuracy. It requires 10-100x fewer gradient evaluations to obtain a comparable quality of approximation.