Extremely Greedy Equivalence Search

The goal of causal discovery is to learn a directed acyclic graph from data. One of the most well-known methods for this problem is Greedy Equivalence Search (GES). GES searches for the graph by incrementally and greedily adding or removing edges to maximize a model selection criterion. It has strong theoretical guarantees on infinite data but can fail in practice on finite data. In this paper, we first identify some of the causes of GES's failure, finding that it can get blocked in local optima, especially in denser graphs. We then propose eXtremely Greedy Equivalent Search (XGES), which involves a new heuristic to improve the search strategy of GES while retaining its theoretical guarantees. In particular, XGES favors deleting edges early in the search over inserting edges, which reduces the possibility of the search ending in local optima. A further contribution of this work is an efficient algorithmic formulation of XGES (and GES). We benchmark XGES on simulated datasets with known ground truth. We find that XGES consistently outperforms GES in recovering the correct graphs, and it is 10 times faster. XGES implementations in Python and C++ are available at https://github.com/ANazaret/XGES.

Hypothesis Testing the Circuit Hypothesis in LLMs

Large language models (LLMs) demonstrate surprising capabilities, but we do not understand how they are implemented. One hypothesis suggests that these capabilities are primarily executed by small subnetworks within the LLM, known as circuits. But how can we evaluate this hypothesis? In this paper, we formalize a set of criteria that a circuit is hypothesized to meet and develop a suite of hypothesis tests to evaluate how well circuits satisfy them. The criteria focus on the extent to which the LLM's behavior is preserved, the degree of localization of this behavior, and whether the circuit is minimal. We apply these tests to six circuits described in the research literature. We find that synthetic circuits -- circuits that are hard-coded in the model -- align with the idealized properties. Circuits discovered in Transformer models satisfy the criteria to varying degrees. To facilitate future empirical studies of circuits, we created the \textit{circuitry} package, a wrapper around the \textit{TransformerLens} library, which abstracts away lower-level manipulations of hooks and activations. The software is available at \url{https://github.com/blei-lab/circuitry}.

Treeffuser: Probabilistic Predictions via Conditional Diffusions with Gradient-Boosted Trees

Probabilistic prediction aims to compute predictive distributions rather than single-point predictions. These distributions enable practitioners to quantify uncertainty, compute risk, and detect outliers. However, most probabilistic methods assume parametric responses, such as Gaussian or Poisson distributions. When these assumptions fail, such models lead to bad predictions and poorly calibrated uncertainty. In this paper, we propose Treeffuser, an easy-to-use method for probabilistic prediction on tabular data. The idea is to learn a conditional diffusion model where the score function is estimated using gradient-boosted trees. The conditional diffusion model makes Treeffuser flexible and non-parametric, while the gradient-boosted trees make it robust and easy to train on CPUs. Treeffuser learns well-calibrated predictive distributions and can handle a wide range of regression tasks -- including those with multivariate, multimodal, and skewed responses. % , as well as categorical predictors and missing data We study Treeffuser on synthetic and real data and show that it outperforms existing methods, providing better-calibrated probabilistic predictions. We further demonstrate its versatility with an application to inventory allocation under uncertainty using sales data from Walmart. We implement Treeffuser in \href{https://github.com/blei-lab/treeffuser}{https://github.com/blei-lab/treeffuser}.

Stable Differentiable Causal Discovery

Inferring causal relationships as directed acyclic graphs (DAGs) is an important but challenging problem. Differentiable Causal Discovery (DCD) is a promising approach to this problem, framing the search as a continuous optimization. But existing DCD methods are numerically unstable, with poor performance beyond tens of variables. In this paper, we propose Stable Differentiable Causal Discovery (SDCD), a new method that improves previous DCD methods in two ways: (1) It employs an alternative constraint for acyclicity; this constraint is more stable, both theoretically and empirically, and fast to compute. (2) It uses a training procedure tailored for sparse causal graphs, which are common in real-world scenarios. We first derive SDCD and prove its stability and correctness. We then evaluate it with both observational and interventional data and on both small-scale and large-scale settings. We find that SDCD outperforms existing methods in both convergence speed and accuracy and can scale to thousands of variables.

The CausalBench challenge: A machine learning contest for gene network inference from single-cell perturbation data

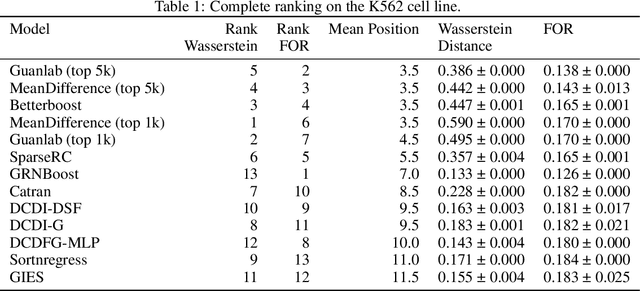
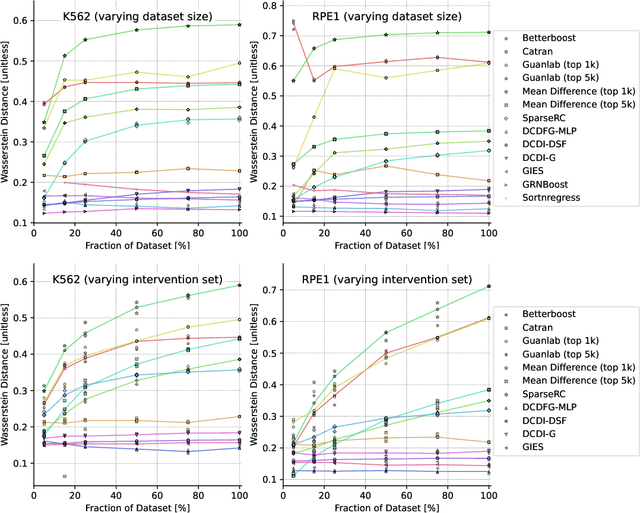
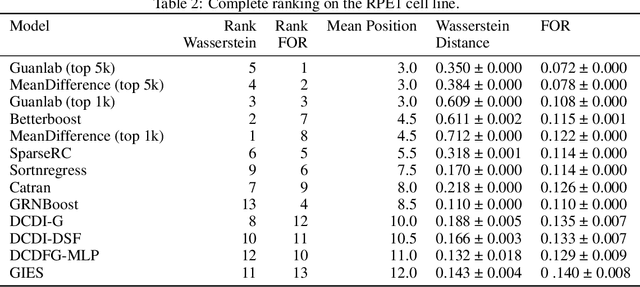
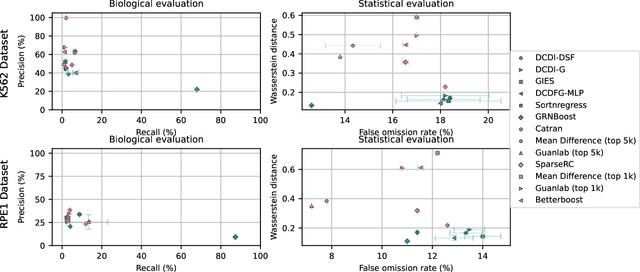
In drug discovery, mapping interactions between genes within cellular systems is a crucial early step. This helps formulate hypotheses regarding molecular mechanisms that could potentially be targeted by future medicines. The CausalBench Challenge was an initiative to invite the machine learning community to advance the state of the art in constructing gene-gene interaction networks. These networks, derived from large-scale, real-world datasets of single cells under various perturbations, are crucial for understanding the causal mechanisms underlying disease biology. Using the framework provided by the CausalBench benchmark, participants were tasked with enhancing the capacity of the state of the art methods to leverage large-scale genetic perturbation data. This report provides an analysis and summary of the methods submitted during the challenge to give a partial image of the state of the art at the time of the challenge. The winning solutions significantly improved performance compared to previous baselines, establishing a new state of the art for this critical task in biology and medicine.

Variational Inference for Infinitely Deep Neural Networks

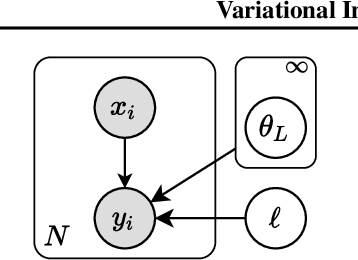
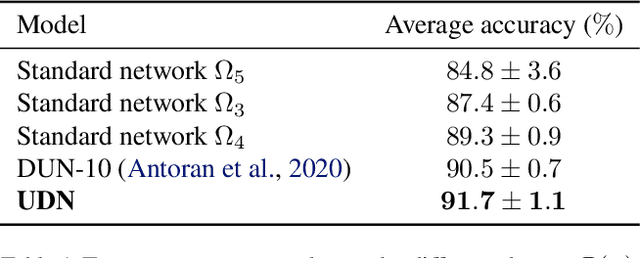
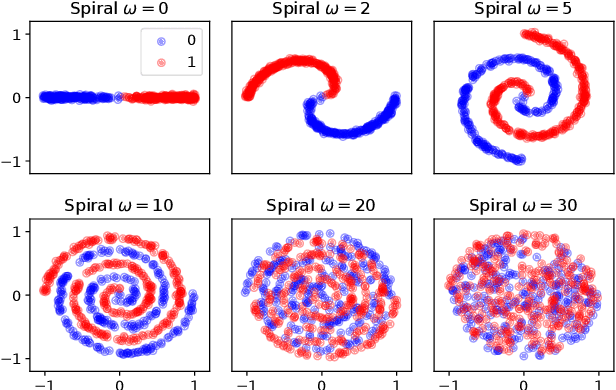
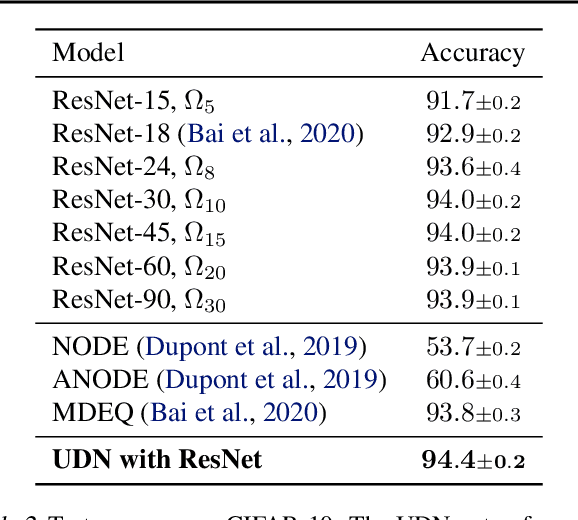
We introduce the unbounded depth neural network (UDN), an infinitely deep probabilistic model that adapts its complexity to the training data. The UDN contains an infinite sequence of hidden layers and places an unbounded prior on a truncation L, the layer from which it produces its data. Given a dataset of observations, the posterior UDN provides a conditional distribution of both the parameters of the infinite neural network and its truncation. We develop a novel variational inference algorithm to approximate this posterior, optimizing a distribution of the neural network weights and of the truncation depth L, and without any upper limit on L. To this end, the variational family has a special structure: it models neural network weights of arbitrary depth, and it dynamically creates or removes free variational parameters as its distribution of the truncation is optimized. (Unlike heuristic approaches to model search, it is solely through gradient-based optimization that this algorithm explores the space of truncations.) We study the UDN on real and synthetic data. We find that the UDN adapts its posterior depth to the dataset complexity; it outperforms standard neural networks of similar computational complexity; and it outperforms other approaches to infinite-depth neural networks.

Stochastic Flows and Geometric Optimization on the Orthogonal Group

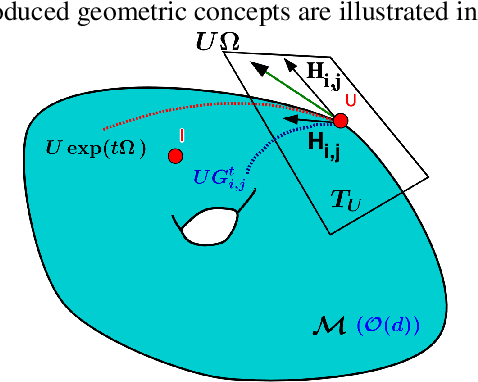
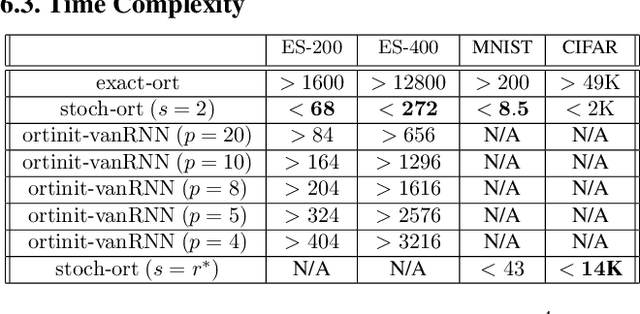
We present a new class of stochastic, geometrically-driven optimization algorithms on the orthogonal group $O(d)$ and naturally reductive homogeneous manifolds obtained from the action of the rotation group $SO(d)$. We theoretically and experimentally demonstrate that our methods can be applied in various fields of machine learning including deep, convolutional and recurrent neural networks, reinforcement learning, normalizing flows and metric learning. We show an intriguing connection between efficient stochastic optimization on the orthogonal group and graph theory (e.g. matching problem, partition functions over graphs, graph-coloring). We leverage the theory of Lie groups and provide theoretical results for the designed class of algorithms. We demonstrate broad applicability of our methods by showing strong performance on the seemingly unrelated tasks of learning world models to obtain stable policies for the most difficult $\mathrm{Humanoid}$ agent from $\mathrm{OpenAI}$ $\mathrm{Gym}$ and improving convolutional neural networks.

A joint model of unpaired data from scRNA-seq and spatial transcriptomics for imputing missing gene expression measurements

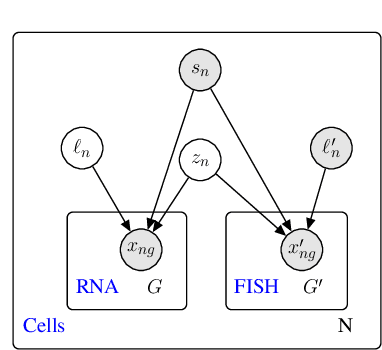
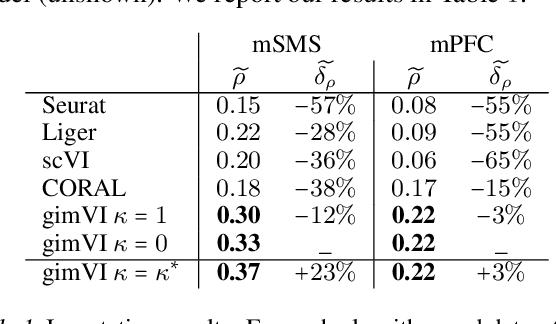
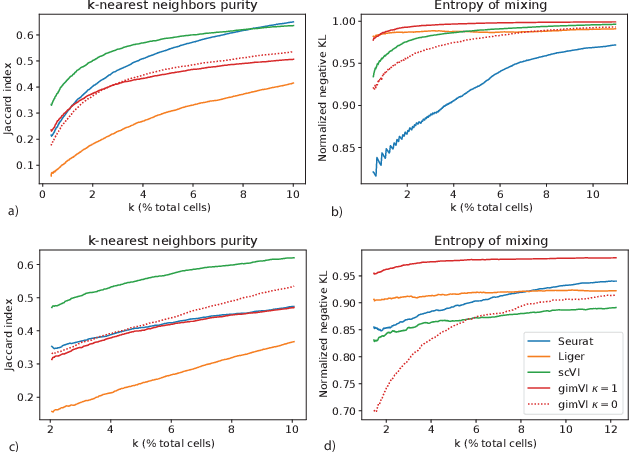
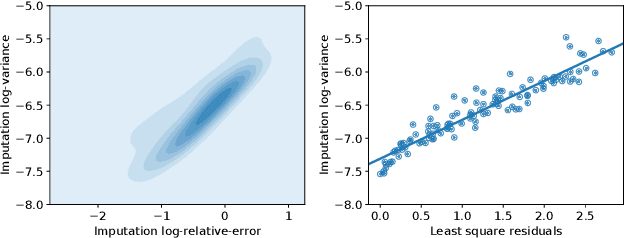
Spatial studies of transcriptome provide biologists with gene expression maps of heterogeneous and complex tissues. However, most experimental protocols for spatial transcriptomics suffer from the need to select beforehand a small fraction of genes to be quantified over the entire transcriptome. Standard single-cell RNA sequencing (scRNA-seq) is more prevalent, easier to implement and can in principle capture any gene but cannot recover the spatial location of the cells. In this manuscript, we focus on the problem of imputation of missing genes in spatial transcriptomic data based on (unpaired) standard scRNA-seq data from the same biological tissue. Building upon domain adaptation work, we propose gimVI, a deep generative model for the integration of spatial transcriptomic data and scRNA-seq data that can be used to impute missing genes. After describing our generative model and an inference procedure for it, we compare gimVI to alternative methods from computational biology or domain adaptation on real datasets and outperform Seurat Anchors, Liger and CORAL to impute held-out genes.