Stochastic Flows and Geometric Optimization on the Orthogonal Group
Paper and Code
Mar 30, 2020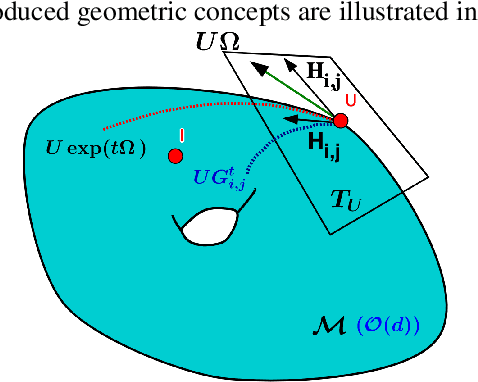
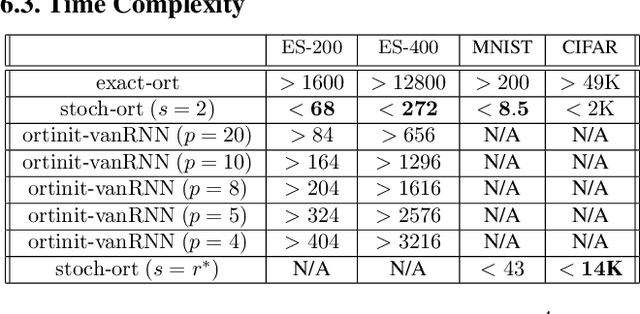


We present a new class of stochastic, geometrically-driven optimization algorithms on the orthogonal group $O(d)$ and naturally reductive homogeneous manifolds obtained from the action of the rotation group $SO(d)$. We theoretically and experimentally demonstrate that our methods can be applied in various fields of machine learning including deep, convolutional and recurrent neural networks, reinforcement learning, normalizing flows and metric learning. We show an intriguing connection between efficient stochastic optimization on the orthogonal group and graph theory (e.g. matching problem, partition functions over graphs, graph-coloring). We leverage the theory of Lie groups and provide theoretical results for the designed class of algorithms. We demonstrate broad applicability of our methods by showing strong performance on the seemingly unrelated tasks of learning world models to obtain stable policies for the most difficult $\mathrm{Humanoid}$ agent from $\mathrm{OpenAI}$ $\mathrm{Gym}$ and improving convolutional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge