Debiasing a First-order Heuristic for Approximate Bi-level Optimization

Approximate bi-level optimization (ABLO) consists of (outer-level) optimization problems, involving numerical (inner-level) optimization loops. While ABLO has many applications across deep learning, it suffers from time and memory complexity proportional to the length $r$ of its inner optimization loop. To address this complexity, an earlier first-order method (FOM) was proposed as a heuristic that omits second derivative terms, yielding significant speed gains and requiring only constant memory. Despite FOM's popularity, there is a lack of theoretical understanding of its convergence properties. We contribute by theoretically characterizing FOM's gradient bias under mild assumptions. We further demonstrate a rich family of examples where FOM-based SGD does not converge to a stationary point of the ABLO objective. We address this concern by proposing an unbiased FOM (UFOM) enjoying constant memory complexity as a function of $r$. We characterize the introduced time-variance tradeoff, demonstrate convergence bounds, and find an optimal UFOM for a given ABLO problem. Finally, we propose an efficient adaptive UFOM scheme.

Sub-Linear Memory: How to Make Performers SLiM

The Transformer architecture has revolutionized deep learning on sequential data, becoming ubiquitous in state-of-the-art solutions for a wide variety of applications. Yet vanilla Transformers are notoriously resource-expensive, requiring $O(L^2)$ in serial time and memory as functions of input length $L$. Recent works proposed various linear self-attention mechanisms, scaling only as $O(L)$ for serial computation. We perform a thorough analysis of recent Transformer mechanisms with linear self-attention, Performers, in terms of overall computational complexity. We observe a remarkable computational flexibility: forward and backward propagation can be performed with no approximations using sublinear memory as a function of $L$ (in addition to negligible storage for the input sequence), at a cost of greater time complexity in the parallel setting. In the extreme case, a Performer consumes only $O(1)$ memory during training, and still requires $O(L)$ time. This discovered time-memory tradeoff can be used for training or, due to complete backward-compatibility, for fine-tuning on a low-memory device, e.g. a smartphone or an earlier-generation GPU, thus contributing towards decentralized and democratized deep learning.

Rethinking Attention with Performers

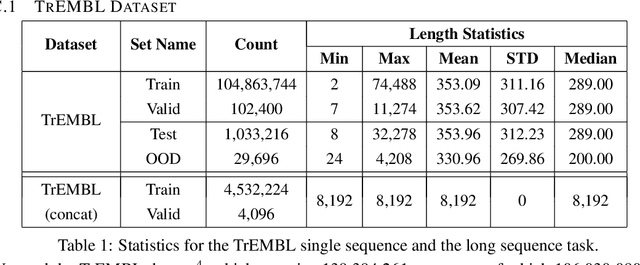
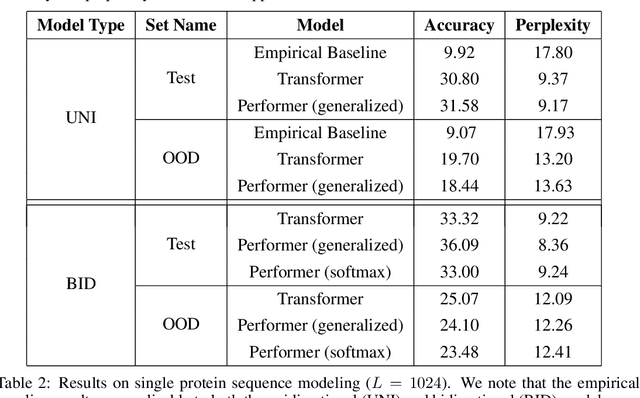
We introduce Performers, Transformer architectures which can estimate regular (softmax) full-rank-attention Transformers with provable accuracy, but using only linear (as opposed to quadratic) space and time complexity, without relying on any priors such as sparsity or low-rankness. To approximate softmax attention-kernels, Performers use a novel Fast Attention Via positive Orthogonal Random features approach (FAVOR+), which may be of independent interest for scalable kernel methods. FAVOR+ can be also used to efficiently model kernelizable attention mechanisms beyond softmax. This representational power is crucial to accurately compare softmax with other kernels for the first time on large-scale tasks, beyond the reach of regular Transformers, and investigate optimal attention-kernels. Performers are linear architectures fully compatible with regular Transformers and with strong theoretical guarantees: unbiased or nearly-unbiased estimation of the attention matrix, uniform convergence and low estimation variance. We tested Performers on a rich set of tasks stretching from pixel-prediction through text models to protein sequence modeling. We demonstrate competitive results with other examined efficient sparse and dense attention methods, showcasing effectiveness of the novel attention-learning paradigm leveraged by Performers.

UFO-BLO: Unbiased First-Order Bilevel Optimization

Bilevel optimization (BLO) is a popular approach with many applications including hyperparameter optimization, neural architecture search, adversarial robustness and model-agnostic meta-learning. However, the approach suffers from time and memory complexity proportional to the length $r$ of its inner optimization loop, which has led to several modifications being proposed. One such modification is \textit{first-order} BLO (FO-BLO) which approximates outer-level gradients by zeroing out second derivative terms, yielding significant speed gains and requiring only constant memory as $r$ varies. Despite FO-BLO's popularity, there is a lack of theoretical understanding of its convergence properties. We make progress by demonstrating a rich family of examples where FO-BLO-based stochastic optimization does not converge to a stationary point of the BLO objective. We address this concern by proposing a new FO-BLO-based unbiased estimate of outer-level gradients, enabling us to theoretically guarantee this convergence, with no harm to memory and expected time complexity. Our findings are supported by experimental results on Omniglot and Mini-ImageNet, popular few-shot meta-learning benchmarks.

Masked Language Modeling for Proteins via Linearly Scalable Long-Context Transformers

Transformer models have achieved state-of-the-art results across a diverse range of domains. However, concern over the cost of training the attention mechanism to learn complex dependencies between distant inputs continues to grow. In response, solutions that exploit the structure and sparsity of the learned attention matrix have blossomed. However, real-world applications that involve long sequences, such as biological sequence analysis, may fall short of meeting these assumptions, precluding exploration of these models. To address this challenge, we present a new Transformer architecture, Performer, based on Fast Attention Via Orthogonal Random features (FAVOR). Our mechanism scales linearly rather than quadratically in the number of tokens in the sequence, is characterized by sub-quadratic space complexity and does not incorporate any sparsity pattern priors. Furthermore, it provides strong theoretical guarantees: unbiased estimation of the attention matrix and uniform convergence. It is also backwards-compatible with pre-trained regular Transformers. We demonstrate its effectiveness on the challenging task of protein sequence modeling and provide detailed theoretical analysis.

CWY Parametrization for Scalable Learning of Orthogonal and Stiefel Matrices

In this paper we propose a new approach for optimization over orthogonal groups. We parametrize an orthogonal matrix as a product of Householder reflections. To overcome low parallelization capabilities of computing Householder reflections sequentially, we employ an accumulation scheme called the compact WY (or CWY) transform---a compact matrix representation for the series of Householder reflections which can be computed efficiently on highly parallelizable computation units such as GPU and TPU. We further introduce the Truncated CWY (or T-CWY)---a novel approach for Stiefel manifold parametrization which has a competitive complexity estimate compared to other methods and, again, has an advantage when computed on GPU and TPU. We apply these proposed parametrizations to train recurrent neural network architectures in the tasks of neural machine translation and video prediction and demonstrate superiority in both computational and learning aspects compared to other methods from the literature.

Stochastic Flows and Geometric Optimization on the Orthogonal Group

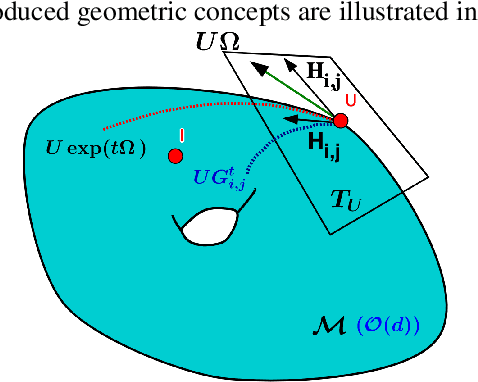
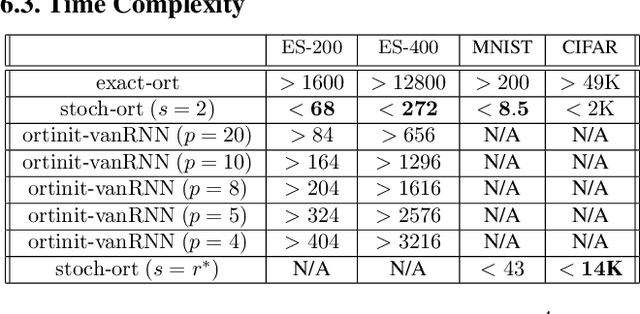
We present a new class of stochastic, geometrically-driven optimization algorithms on the orthogonal group $O(d)$ and naturally reductive homogeneous manifolds obtained from the action of the rotation group $SO(d)$. We theoretically and experimentally demonstrate that our methods can be applied in various fields of machine learning including deep, convolutional and recurrent neural networks, reinforcement learning, normalizing flows and metric learning. We show an intriguing connection between efficient stochastic optimization on the orthogonal group and graph theory (e.g. matching problem, partition functions over graphs, graph-coloring). We leverage the theory of Lie groups and provide theoretical results for the designed class of algorithms. We demonstrate broad applicability of our methods by showing strong performance on the seemingly unrelated tasks of learning world models to obtain stable policies for the most difficult $\mathrm{Humanoid}$ agent from $\mathrm{OpenAI}$ $\mathrm{Gym}$ and improving convolutional neural networks.