On the Limited Representational Power of Value Functions and its Links to Statistical (In)Efficiency

Identifying the trade-offs between model-based and model-free methods is a central question in reinforcement learning. Value-based methods offer substantial computational advantages and are sometimes just as statistically efficient as model-based methods. However, focusing on the core problem of policy evaluation, we show information about the transition dynamics may be impossible to represent in the space of value functions. We explore this through a series of case studies focused on structures that arises in many important problems. In several, there is no information loss and value-based methods are as statistically efficient as model based ones. In other closely-related examples, information loss is severe and value-based methods are severely outperformed. A deeper investigation points to the limitations of the representational power as the driver of the inefficiency, as opposed to failure in algorithm design.

On the Statistical Benefits of Temporal Difference Learning

Given a dataset on actions and resulting long-term rewards, a direct estimation approach fits value functions that minimize prediction error on the training data. Temporal difference learning (TD) methods instead fit value functions by minimizing the degree of temporal inconsistency between estimates made at successive time-steps. Focusing on finite state Markov chains, we provide a crisp asymptotic theory of the statistical advantages of this approach. First, we show that an intuitive inverse trajectory pooling coefficient completely characterizes the percent reduction in mean-squared error of value estimates. Depending on problem structure, the reduction could be enormous or nonexistent. Next, we prove that there can be dramatic improvements in estimates of the difference in value-to-go for two states: TD's errors are bounded in terms of a novel measure - the problem's trajectory crossing time - which can be much smaller than the problem's time horizon.

Stochastic Flows and Geometric Optimization on the Orthogonal Group

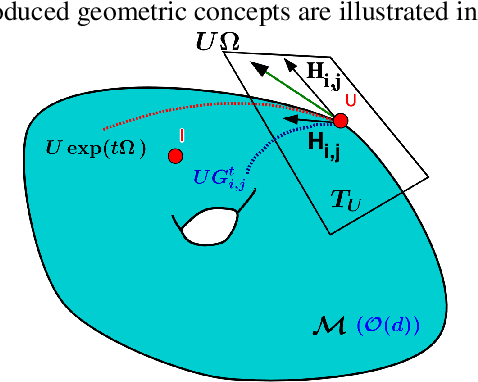
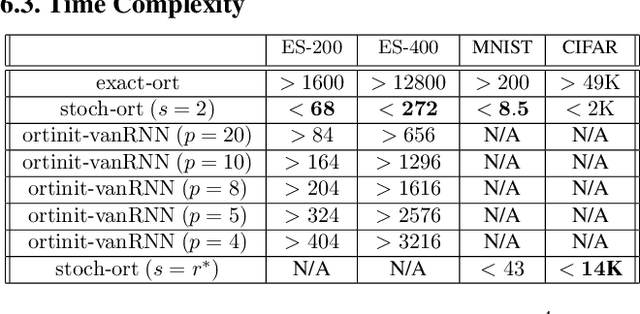
We present a new class of stochastic, geometrically-driven optimization algorithms on the orthogonal group $O(d)$ and naturally reductive homogeneous manifolds obtained from the action of the rotation group $SO(d)$. We theoretically and experimentally demonstrate that our methods can be applied in various fields of machine learning including deep, convolutional and recurrent neural networks, reinforcement learning, normalizing flows and metric learning. We show an intriguing connection between efficient stochastic optimization on the orthogonal group and graph theory (e.g. matching problem, partition functions over graphs, graph-coloring). We leverage the theory of Lie groups and provide theoretical results for the designed class of algorithms. We demonstrate broad applicability of our methods by showing strong performance on the seemingly unrelated tasks of learning world models to obtain stable policies for the most difficult $\mathrm{Humanoid}$ agent from $\mathrm{OpenAI}$ $\mathrm{Gym}$ and improving convolutional neural networks.