Can Generative AI Solve Your In-Context Learning Problem? A Martingale Perspective

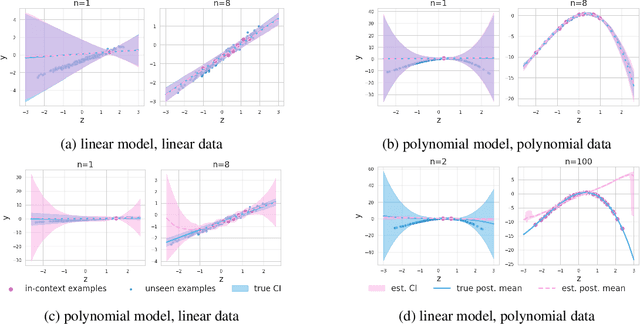
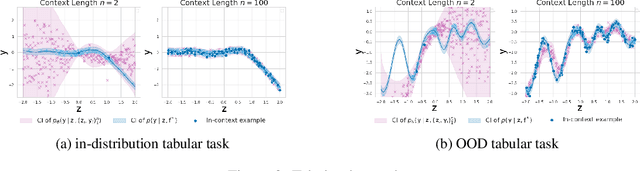
This work is about estimating when a conditional generative model (CGM) can solve an in-context learning (ICL) problem. An in-context learning (ICL) problem comprises a CGM, a dataset, and a prediction task. The CGM could be a multi-modal foundation model; the dataset, a collection of patient histories, test results, and recorded diagnoses; and the prediction task to communicate a diagnosis to a new patient. A Bayesian interpretation of ICL assumes that the CGM computes a posterior predictive distribution over an unknown Bayesian model defining a joint distribution over latent explanations and observable data. From this perspective, Bayesian model criticism is a reasonable approach to assess the suitability of a given CGM for an ICL problem. However, such approaches -- like posterior predictive checks (PPCs) -- often assume that we can sample from the likelihood and posterior defined by the Bayesian model, which are not explicitly given for contemporary CGMs. To address this, we show when ancestral sampling from the predictive distribution of a CGM is equivalent to sampling datasets from the posterior predictive of the assumed Bayesian model. Then we develop the generative predictive $p$-value, which enables PPCs and their cousins for contemporary CGMs. The generative predictive $p$-value can then be used in a statistical decision procedure to determine when the model is appropriate for an ICL problem. Our method only requires generating queries and responses from a CGM and evaluating its response log probability. We empirically evaluate our method on synthetic tabular, imaging, and natural language ICL tasks using large language models.

Hypothesis Testing the Circuit Hypothesis in LLMs

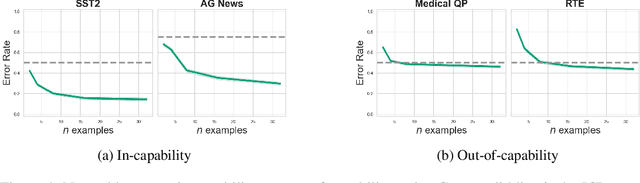
Large language models (LLMs) demonstrate surprising capabilities, but we do not understand how they are implemented. One hypothesis suggests that these capabilities are primarily executed by small subnetworks within the LLM, known as circuits. But how can we evaluate this hypothesis? In this paper, we formalize a set of criteria that a circuit is hypothesized to meet and develop a suite of hypothesis tests to evaluate how well circuits satisfy them. The criteria focus on the extent to which the LLM's behavior is preserved, the degree of localization of this behavior, and whether the circuit is minimal. We apply these tests to six circuits described in the research literature. We find that synthetic circuits -- circuits that are hard-coded in the model -- align with the idealized properties. Circuits discovered in Transformer models satisfy the criteria to varying degrees. To facilitate future empirical studies of circuits, we created the \textit{circuitry} package, a wrapper around the \textit{TransformerLens} library, which abstracts away lower-level manipulations of hooks and activations. The software is available at \url{https://github.com/blei-lab/circuitry}.

Improving Generalization on the ProcGen Benchmark with Simple Architectural Changes and Scale

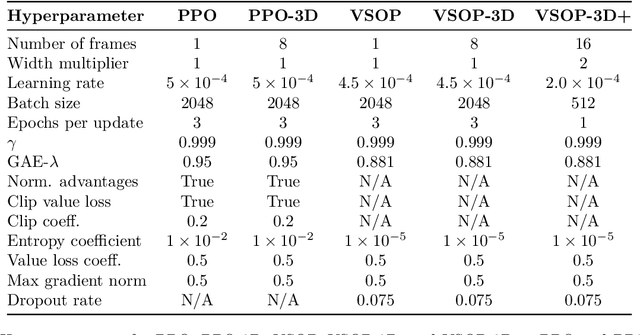
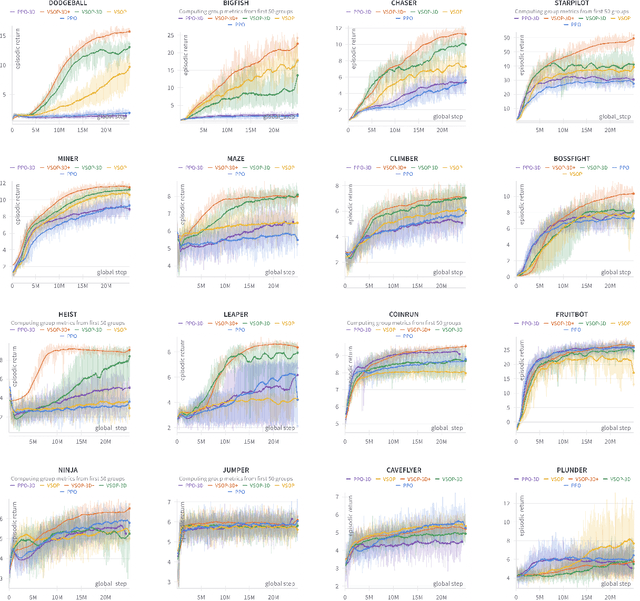
We demonstrate that recent advances in reinforcement learning (RL) combined with simple architectural changes significantly improves generalization on the ProcGen benchmark. These changes are frame stacking, replacing 2D convolutional layers with 3D convolutional layers, and scaling up the number of convolutional kernels per layer. Experimental results using a single set of hyperparameters across all environments show a 37.9\% reduction in the optimality gap compared to the baseline (from 0.58 to 0.36). This performance matches or exceeds current state-of-the-art methods. The proposed changes are largely orthogonal and therefore complementary to the existing approaches for improving generalization in RL, and our results suggest that further exploration in this direction could yield substantial improvements in addressing generalization challenges in deep reinforcement learning.

Estimating the Hallucination Rate of Generative AI

This work is about estimating the hallucination rate for in-context learning (ICL) with Generative AI. In ICL, a conditional generative model (CGM) is prompted with a dataset and asked to make a prediction based on that dataset. The Bayesian interpretation of ICL assumes that the CGM is calculating a posterior predictive distribution over an unknown Bayesian model of a latent parameter and data. With this perspective, we define a \textit{hallucination} as a generated prediction that has low-probability under the true latent parameter. We develop a new method that takes an ICL problem -- that is, a CGM, a dataset, and a prediction question -- and estimates the probability that a CGM will generate a hallucination. Our method only requires generating queries and responses from the model and evaluating its response log probability. We empirically evaluate our method on synthetic regression and natural language ICL tasks using large language models.

DiscoBAX: Discovery of Optimal Intervention Sets in Genomic Experiment Design

The discovery of therapeutics to treat genetically-driven pathologies relies on identifying genes involved in the underlying disease mechanisms. Existing approaches search over the billions of potential interventions to maximize the expected influence on the target phenotype. However, to reduce the risk of failure in future stages of trials, practical experiment design aims to find a set of interventions that maximally change a target phenotype via diverse mechanisms. We propose DiscoBAX, a sample-efficient method for maximizing the rate of significant discoveries per experiment while simultaneously probing for a wide range of diverse mechanisms during a genomic experiment campaign. We provide theoretical guarantees of approximate optimality under standard assumptions, and conduct a comprehensive experimental evaluation covering both synthetic as well as real-world experimental design tasks. DiscoBAX outperforms existing state-of-the-art methods for experimental design, selecting effective and diverse perturbations in biological systems.

BatchGFN: Generative Flow Networks for Batch Active Learning

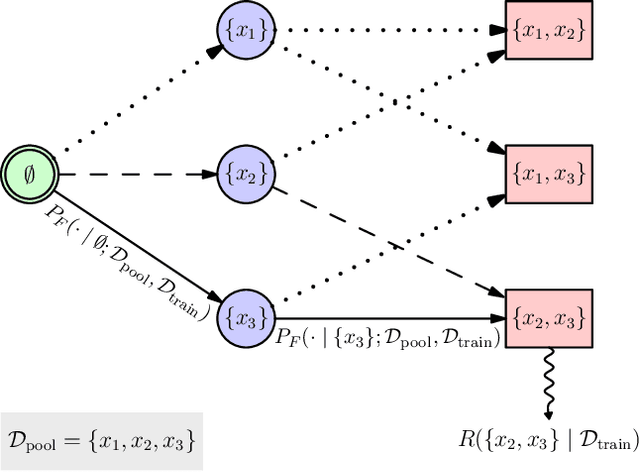
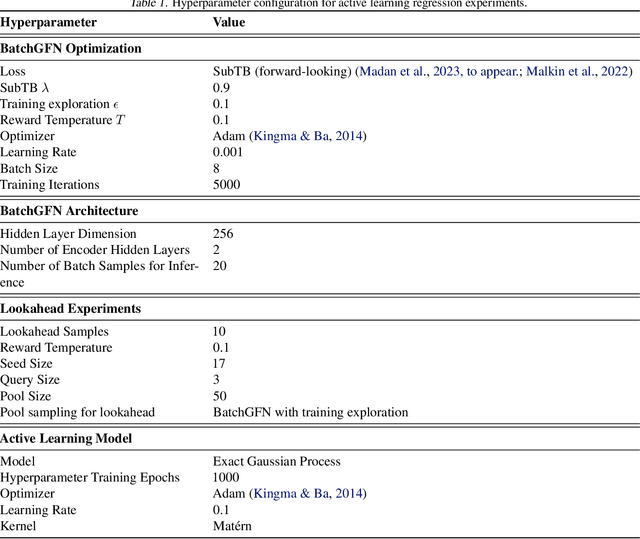
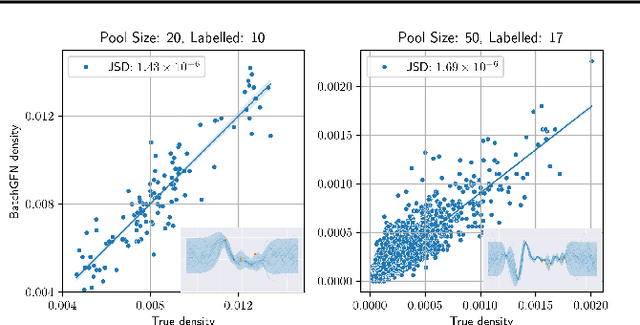
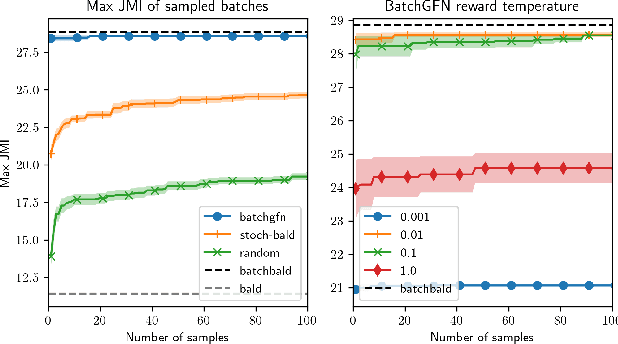
We introduce BatchGFN -- a novel approach for pool-based active learning that uses generative flow networks to sample sets of data points proportional to a batch reward. With an appropriate reward function to quantify the utility of acquiring a batch, such as the joint mutual information between the batch and the model parameters, BatchGFN is able to construct highly informative batches for active learning in a principled way. We show our approach enables sampling near-optimal utility batches at inference time with a single forward pass per point in the batch in toy regression problems. This alleviates the computational complexity of batch-aware algorithms and removes the need for greedy approximations to find maximizers for the batch reward. We also present early results for amortizing training across acquisition steps, which will enable scaling to real-world tasks.

ReLU to the Rescue: Improve Your On-Policy Actor-Critic with Positive Advantages

This paper introduces a novel method for enhancing the effectiveness of on-policy Deep Reinforcement Learning (DRL) algorithms. Three surprisingly simple modifications to the A3C algorithm: (1) processing advantage estimates through a ReLU function, (2) spectral normalization, and (3) dropout, serve to not only improve efficacy but also yield a ``cautious'' DRL algorithm. Where on-policy algorithms such as Proximal Policy Optimization (PPO) and Asynchronous Advantage Actor-Critic (A3C) do not explicitly account for cautious interaction with the environment, our method integrates caution in two critical ways: (1) by maximizing a lower bound on the value function plus a constant, thereby promoting a \textit{conservative value estimation}, and (2) by incorporating Thompson sampling for cautious exploration. In proving that our algorithm maximizes the lower bound, we also ground Regret Matching Policy Gradients (RMPG), a discrete-action on-policy method for multi-agent reinforcement learning. Our rigorous empirical evaluations across various benchmarks demonstrate our approach's improved performance against existing on-policy algorithms. This research represents a substantial step towards efficacious and cautious DRL algorithms, which are needed to unlock applications to complex, real-world problems.

B-Learner: Quasi-Oracle Bounds on Heterogeneous Causal Effects Under Hidden Confounding

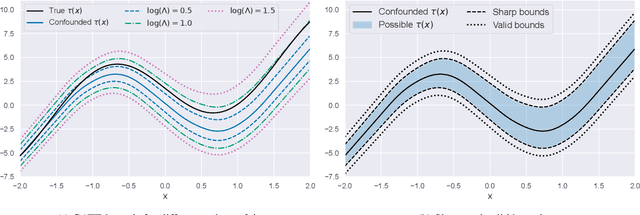
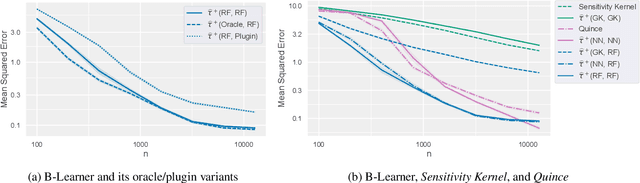
Estimating heterogeneous treatment effects from observational data is a crucial task across many fields, helping policy and decision-makers take better actions. There has been recent progress on robust and efficient methods for estimating the conditional average treatment effect (CATE) function, but these methods often do not take into account the risk of hidden confounding, which could arbitrarily and unknowingly bias any causal estimate based on observational data. We propose a meta-learner called the B-Learner, which can efficiently learn sharp bounds on the CATE function under limits on the level of hidden confounding. We derive the B-Learner by adapting recent results for sharp and valid bounds of the average treatment effect (Dorn et al., 2021) into the framework given by Kallus & Oprescu (2022) for robust and model-agnostic learning of distributional treatment effects. The B-Learner can use any function estimator such as random forests and deep neural networks, and we prove its estimates are valid, sharp, efficient, and have a quasi-oracle property with respect to the constituent estimators under more general conditions than existing methods. Semi-synthetic experimental comparisons validate the theoretical findings, and we use real-world data demonstrate how the method might be used in practice.

Differentiable Multi-Target Causal Bayesian Experimental Design

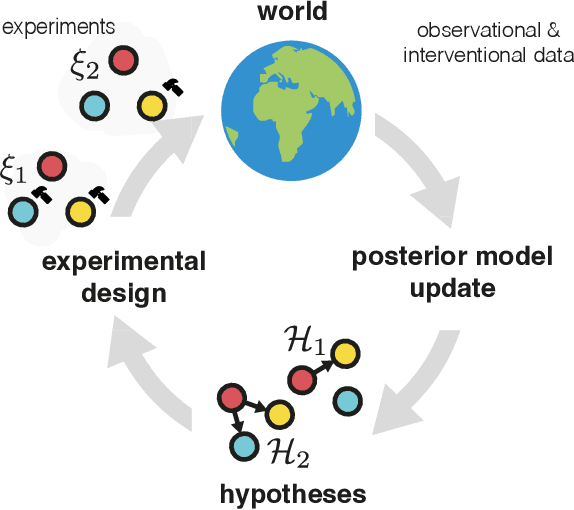
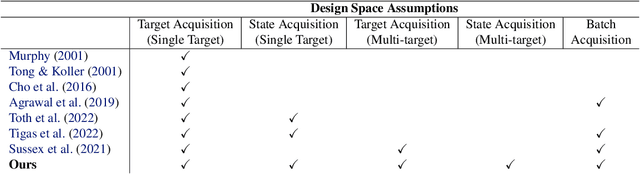
We introduce a gradient-based approach for the problem of Bayesian optimal experimental design to learn causal models in a batch setting -- a critical component for causal discovery from finite data where interventions can be costly or risky. Existing methods rely on greedy approximations to construct a batch of experiments while using black-box methods to optimize over a single target-state pair to intervene with. In this work, we completely dispose of the black-box optimization techniques and greedy heuristics and instead propose a conceptually simple end-to-end gradient-based optimization procedure to acquire a set of optimal intervention target-state pairs. Such a procedure enables parameterization of the design space to efficiently optimize over a batch of multi-target-state interventions, a setting which has hitherto not been explored due to its complexity. We demonstrate that our proposed method outperforms baselines and existing acquisition strategies in both single-target and multi-target settings across a number of synthetic datasets.

Scalable Sensitivity and Uncertainty Analysis for Causal-Effect Estimates of Continuous-Valued Interventions

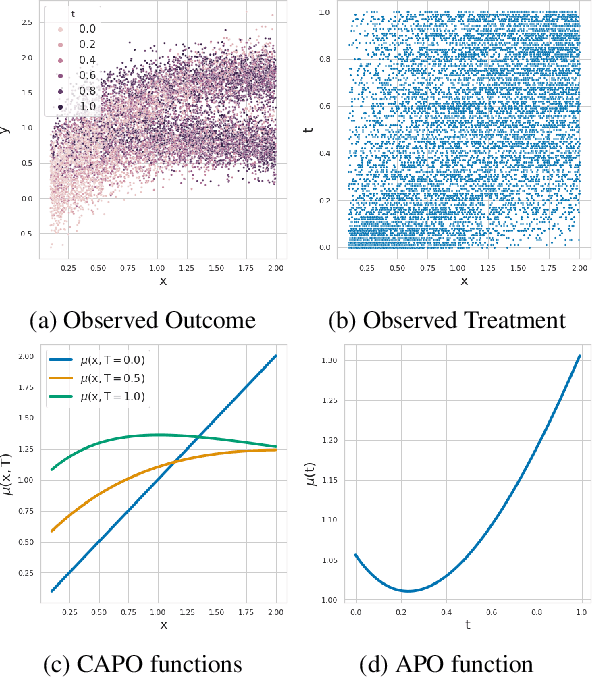
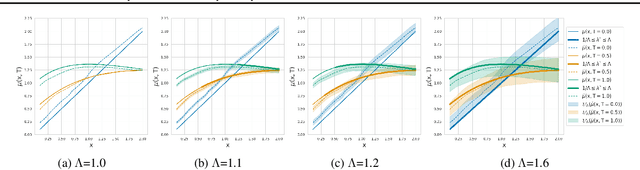
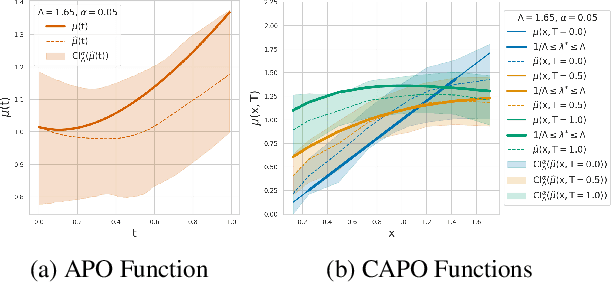
Estimating the effects of continuous-valued interventions from observational data is critically important in fields such as climate science, healthcare, and economics. Recent work focuses on designing neural-network architectures and regularization functions to allow for scalable estimation of average and individual-level dose response curves from high-dimensional, large-sample data. Such methodologies assume ignorability (all confounding variables are observed) and positivity (all levels of treatment can be observed for every unit described by a given covariate value), which are especially challenged in the continuous treatment regime. Developing scalable sensitivity and uncertainty analyses that allow us to understand the ignorance induced in our estimates when these assumptions are relaxed receives less attention. Here, we develop a continuous treatment-effect marginal sensitivity model (CMSM) and derive bounds that agree with both the observed data and a researcher-defined level of hidden confounding. We introduce a scalable algorithm to derive the bounds and uncertainty-aware deep models to efficiently estimate these bounds for high-dimensional, large-sample observational data. We validate our methods using both synthetic and real-world experiments. For the latter, we work in concert with climate scientists interested in evaluating the climatological impacts of human emissions on cloud properties using satellite observations from the past 15 years: a finite-data problem known to be complicated by the presence of a multitude of unobserved confounders.