B-Learner: Quasi-Oracle Bounds on Heterogeneous Causal Effects Under Hidden Confounding

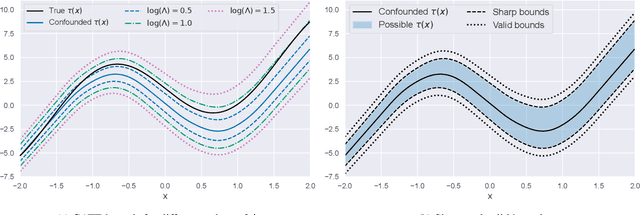
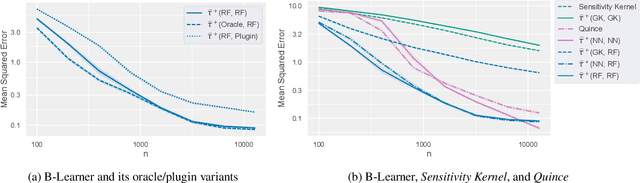
Estimating heterogeneous treatment effects from observational data is a crucial task across many fields, helping policy and decision-makers take better actions. There has been recent progress on robust and efficient methods for estimating the conditional average treatment effect (CATE) function, but these methods often do not take into account the risk of hidden confounding, which could arbitrarily and unknowingly bias any causal estimate based on observational data. We propose a meta-learner called the B-Learner, which can efficiently learn sharp bounds on the CATE function under limits on the level of hidden confounding. We derive the B-Learner by adapting recent results for sharp and valid bounds of the average treatment effect (Dorn et al., 2021) into the framework given by Kallus & Oprescu (2022) for robust and model-agnostic learning of distributional treatment effects. The B-Learner can use any function estimator such as random forests and deep neural networks, and we prove its estimates are valid, sharp, efficient, and have a quasi-oracle property with respect to the constituent estimators under more general conditions than existing methods. Semi-synthetic experimental comparisons validate the theoretical findings, and we use real-world data demonstrate how the method might be used in practice.

Doubly-Valid/Doubly-Sharp Sensitivity Analysis for Causal Inference with Unmeasured Confounding

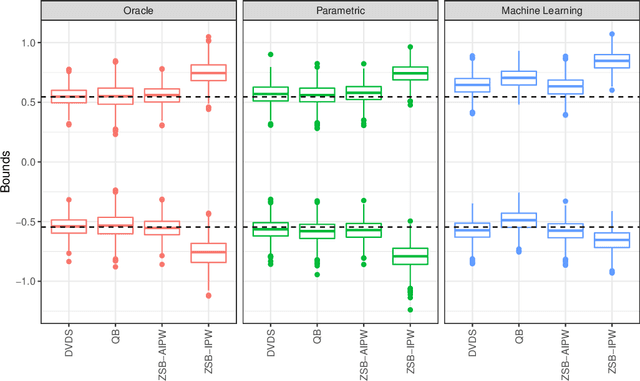
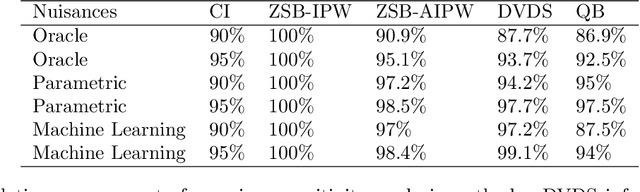
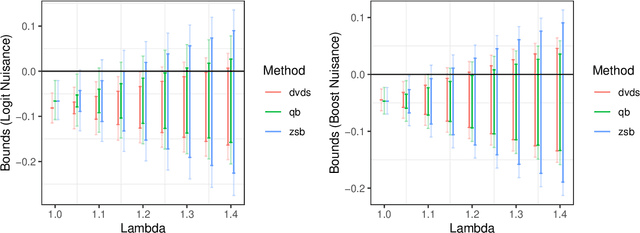
We study the problem of constructing bounds on the average treatment effect in the presence of unobserved confounding under the marginal sensitivity model of Tan (2006). Combining an existing characterization involving adversarial propensity scores with a new distributionally robust characterization of the problem, we propose novel estimators of these bounds that we call "doubly-valid/doubly-sharp" (DVDS) estimators. Double sharpness corresponds to the fact that DVDS estimators consistently estimate the tightest possible (i.e., sharp) bounds implied by the sensitivity model even when one of two nuisance parameters is misspecified and achieve semiparametric efficiency when all nuisance parameters are suitably consistent. Double validity is an entirely new property for partial identification: DVDS estimators still provide valid, though not sharp, bounds even when most nuisance parameters are misspecified. In fact, even in cases when DVDS point estimates fail to be asymptotically normal, standard Wald confidence intervals may remain valid. In the case of binary outcomes, the DVDS estimators are particularly convenient and possesses a closed-form expression in terms of the outcome regression and propensity score. We demonstrate the DVDS estimators in a simulation study as well as a case study of right heart catheterization.