John Cunningham
Variational Nearest Neighbor Gaussian Processes
Feb 03, 2022



Abstract:Variational approximations to Gaussian processes (GPs) typically use a small set of inducing points to form a low-rank approximation to the covariance matrix. In this work, we instead exploit a sparse approximation of the precision matrix. We propose variational nearest neighbor Gaussian process (VNNGP), which introduces a prior that only retains correlations within K nearest-neighboring observations, thereby inducing sparse precision structure. Using the variational framework, VNNGP's objective can be factorized over both observations and inducing points, enabling stochastic optimization with a time complexity of O($K^3$). Hence, we can arbitrarily scale the inducing point size, even to the point of putting inducing points at every observed location. We compare VNNGP to other scalable GPs through various experiments, and demonstrate that VNNGP (1) can dramatically outperform low-rank methods, and (2) is less prone to overfitting than other nearest neighbor methods.
Hierarchical Inducing Point Gaussian Process for Inter-domain Observations
Feb 28, 2021
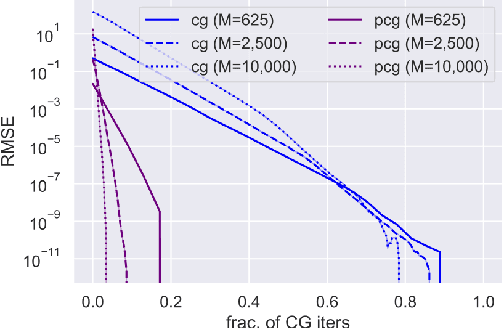
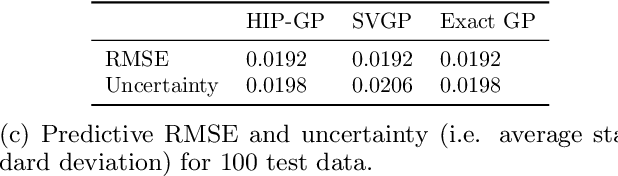
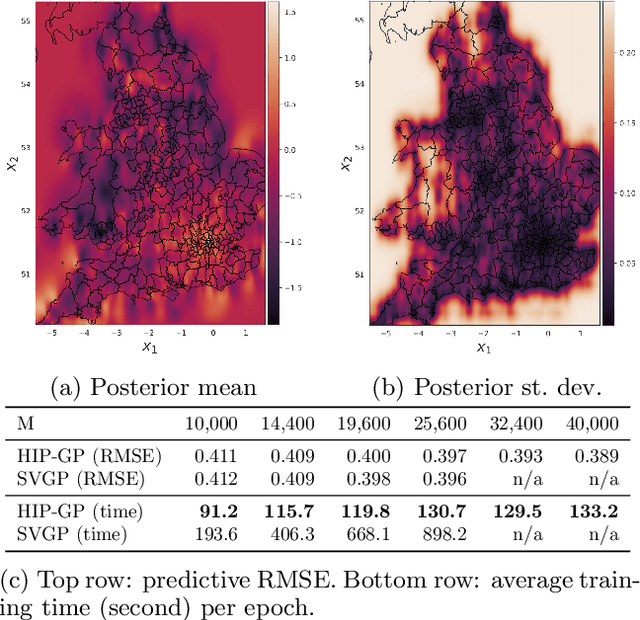
Abstract:We examine the general problem of inter-domain Gaussian Processes (GPs): problems where the GP realization and the noisy observations of that realization lie on different domains. When the mapping between those domains is linear, such as integration or differentiation, inference is still closed form. However, many of the scaling and approximation techniques that our community has developed do not apply to this setting. In this work, we introduce the hierarchical inducing point GP (HIP-GP), a scalable inter-domain GP inference method that enables us to improve the approximation accuracy by increasing the number of inducing points to the millions. HIP-GP, which relies on inducing points with grid structure and a stationary kernel assumption, is suitable for low-dimensional problems. In developing HIP-GP, we introduce (1) a fast whitening strategy, and (2) a novel preconditioner for conjugate gradients which can be helpful in general GP settings.
A Novel Variational Family for Hidden Nonlinear Markov Models
Nov 06, 2018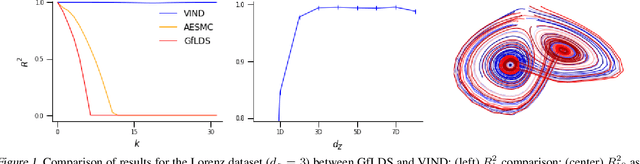
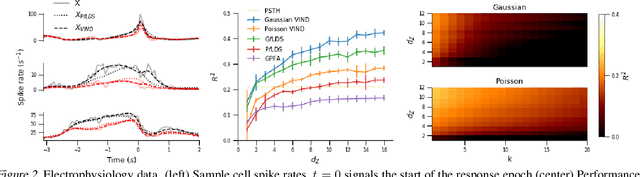
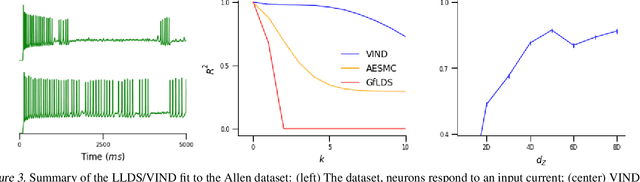
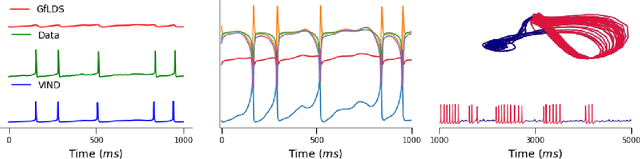
Abstract:Latent variable models have been widely applied for the analysis and visualization of large datasets. In the case of sequential data, closed-form inference is possible when the transition and observation functions are linear. However, approximate inference techniques are usually necessary when dealing with nonlinear dynamics and observation functions. Here, we propose a novel variational inference framework for the explicit modeling of time series, Variational Inference for Nonlinear Dynamics (VIND), that is able to uncover nonlinear observation and transition functions from sequential data. The framework includes a structured approximate posterior, and an algorithm that relies on the fixed-point iteration method to find the best estimate for latent trajectories. We apply the method to several datasets and show that it is able to accurately infer the underlying dynamics of these systems, in some cases substantially outperforming state-of-the-art methods.
Black box variational inference for state space models
Nov 23, 2015



Abstract:Latent variable time-series models are among the most heavily used tools from machine learning and applied statistics. These models have the advantage of learning latent structure both from noisy observations and from the temporal ordering in the data, where it is assumed that meaningful correlation structure exists across time. A few highly-structured models, such as the linear dynamical system with linear-Gaussian observations, have closed-form inference procedures (e.g. the Kalman Filter), but this case is an exception to the general rule that exact posterior inference in more complex generative models is intractable. Consequently, much work in time-series modeling focuses on approximate inference procedures for one particular class of models. Here, we extend recent developments in stochastic variational inference to develop a `black-box' approximate inference technique for latent variable models with latent dynamical structure. We propose a structured Gaussian variational approximate posterior that carries the same intuition as the standard Kalman filter-smoother but, importantly, permits us to use the same inference approach to approximate the posterior of much more general, nonlinear latent variable generative models. We show that our approach recovers accurate estimates in the case of basic models with closed-form posteriors, and more interestingly performs well in comparison to variational approaches that were designed in a bespoke fashion for specific non-conjugate models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge