Hierarchical Inducing Point Gaussian Process for Inter-domain Observations

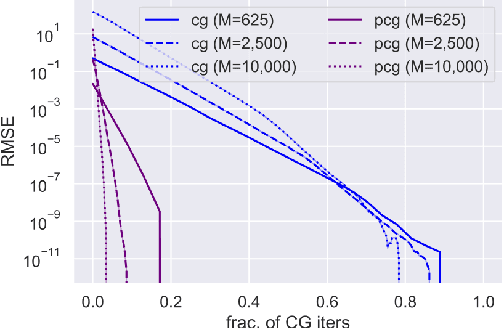
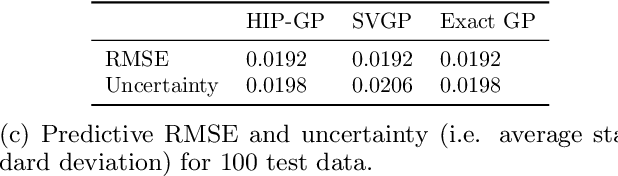
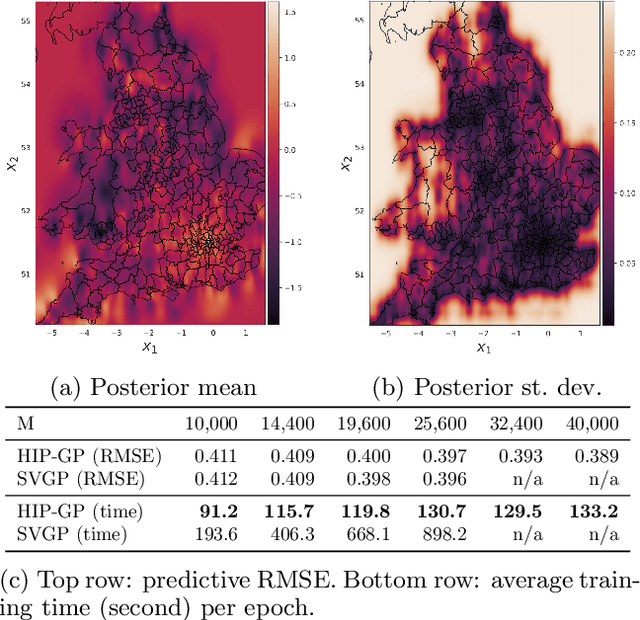
We examine the general problem of inter-domain Gaussian Processes (GPs): problems where the GP realization and the noisy observations of that realization lie on different domains. When the mapping between those domains is linear, such as integration or differentiation, inference is still closed form. However, many of the scaling and approximation techniques that our community has developed do not apply to this setting. In this work, we introduce the hierarchical inducing point GP (HIP-GP), a scalable inter-domain GP inference method that enables us to improve the approximation accuracy by increasing the number of inducing points to the millions. HIP-GP, which relies on inducing points with grid structure and a stationary kernel assumption, is suitable for low-dimensional problems. In developing HIP-GP, we introduce (1) a fast whitening strategy, and (2) a novel preconditioner for conjugate gradients which can be helpful in general GP settings.

Modeling the Gaia Color-Magnitude Diagram with Bayesian Neural Flows to Constrain Distance Estimates

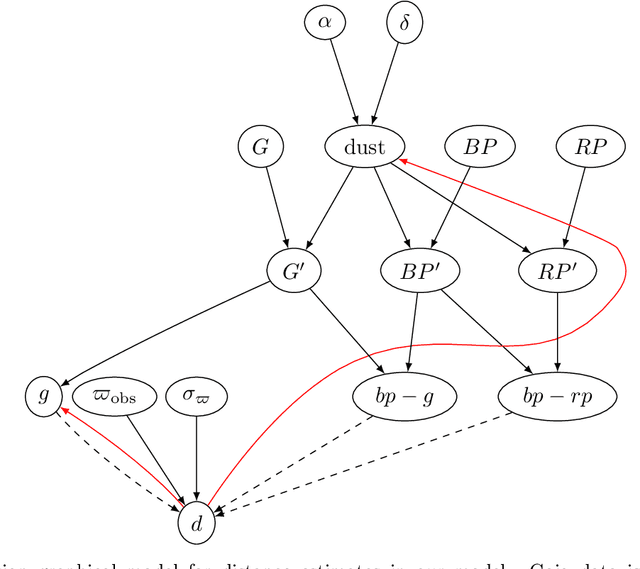
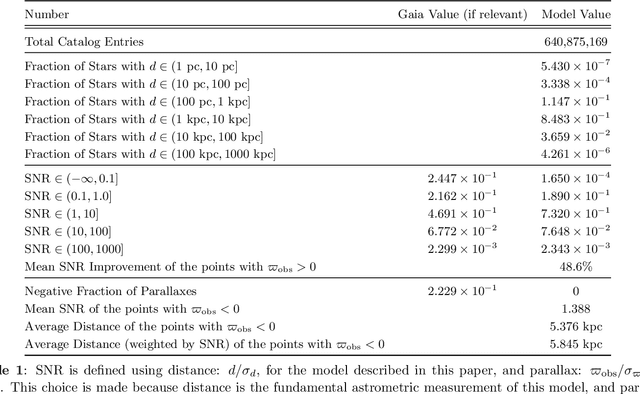
We demonstrate an algorithm for learning a flexible color-magnitude diagram from noisy parallax and photometry measurements using a normalizing flow, a deep neural network capable of learning an arbitrary multi-dimensional probability distribution. We present a catalog of 640M photometric distance posteriors to nearby stars derived from this data-driven model using Gaia DR2 photometry and parallaxes. Dust estimation and dereddening is done iteratively inside the model and without prior distance information, using the Bayestar map. The signal-to-noise (precision) of distance measurements improves on average by more than 48% over the raw Gaia data, and we also demonstrate how the accuracy of distances have improved over other models, especially in the noisy-parallax regime. Applications are discussed, including significantly improved Milky Way disk separation and substructure detection. We conclude with a discussion of future work, which exploits the normalizing flow architecture to allow us to exactly marginalize over missing photometry, enabling the inclusion of many surveys without losing coverage.