Energy-Weighted Flow Matching: Unlocking Continuous Normalizing Flows for Efficient and Scalable Boltzmann Sampling

Sampling from unnormalized target distributions, e.g. Boltzmann distributions $\mu_{\text{target}}(x) \propto \exp(-E(x)/T)$, is fundamental to many scientific applications yet computationally challenging due to complex, high-dimensional energy landscapes. Existing approaches applying modern generative models to Boltzmann distributions either require large datasets of samples drawn from the target distribution or, when using only energy evaluations for training, cannot efficiently leverage the expressivity of advanced architectures like continuous normalizing flows that have shown promise for molecular sampling. To address these shortcomings, we introduce Energy-Weighted Flow Matching (EWFM), a novel training objective enabling continuous normalizing flows to model Boltzmann distributions using only energy function evaluations. Our objective reformulates conditional flow matching via importance sampling, allowing training with samples from arbitrary proposal distributions. Based on this objective, we develop two algorithms: iterative EWFM (iEWFM), which progressively refines proposals through iterative training, and annealed EWFM (aEWFM), which additionally incorporates temperature annealing for challenging energy landscapes. On benchmark systems, including challenging 55-particle Lennard-Jones clusters, our algorithms demonstrate sample quality competitive with state-of-the-art energy-only methods while requiring up to three orders of magnitude fewer energy evaluations.

Theoretical Limitations of Ensembles in the Age of Overparameterization

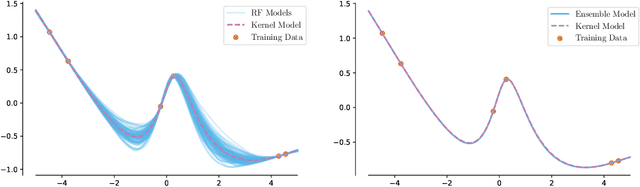
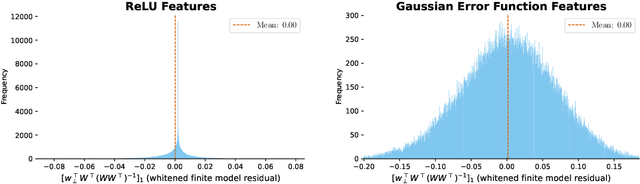
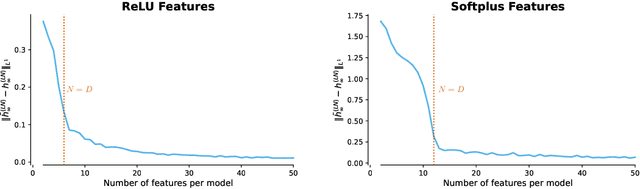
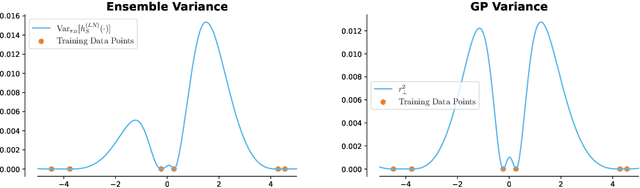
Classic tree-based ensembles generalize better than any single decision tree. In contrast, recent empirical studies find that modern ensembles of (overparameterized) neural networks may not provide any inherent generalization advantage over single but larger neural networks. This paper clarifies how modern overparameterized ensembles differ from their classic underparameterized counterparts, using ensembles of random feature (RF) regressors as a basis for developing theory. In contrast to the underparameterized regime, where ensembling typically induces regularization and increases generalization, we prove that infinite ensembles of overparameterized RF regressors become pointwise equivalent to (single) infinite-width RF regressors. This equivalence, which is exact for ridgeless models and approximate for small ridge penalties, implies that overparameterized ensembles and single large models exhibit nearly identical generalization. As a consequence, we can characterize the predictive variance amongst ensemble members, and demonstrate that it quantifies the expected effects of increasing capacity rather than capturing any conventional notion of uncertainty. Our results challenge common assumptions about the advantages of ensembles in overparameterized settings, prompting a reconsideration of how well intuitions from underparameterized ensembles transfer to deep ensembles and the overparameterized regime.

Targeted Sequential Indirect Experiment Design

Scientific hypotheses typically concern specific aspects of complex, imperfectly understood or entirely unknown mechanisms, such as the effect of gene expression levels on phenotypes or how microbial communities influence environmental health. Such queries are inherently causal (rather than purely associational), but in many settings, experiments can not be conducted directly on the target variables of interest, but are indirect. Therefore, they perturb the target variable, but do not remove potential confounding factors. If, additionally, the resulting experimental measurements are multi-dimensional and the studied mechanisms nonlinear, the query of interest is generally not identified. We develop an adaptive strategy to design indirect experiments that optimally inform a targeted query about the ground truth mechanism in terms of sequentially narrowing the gap between an upper and lower bound on the query. While the general formulation consists of a bi-level optimization procedure, we derive an efficiently estimable analytical kernel-based estimator of the bounds for the causal effect, a query of key interest, and demonstrate the efficacy of our approach in confounded, multivariate, nonlinear synthetic settings.

Sumformer: Universal Approximation for Efficient Transformers

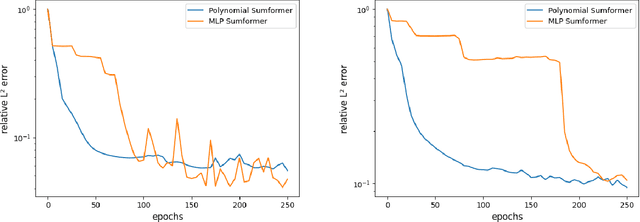
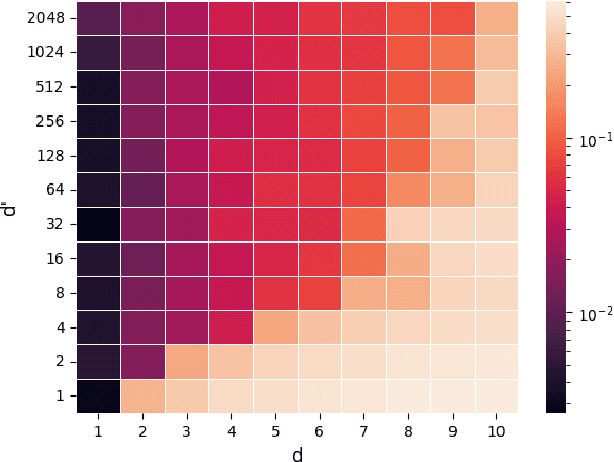
Natural language processing (NLP) made an impressive jump with the introduction of Transformers. ChatGPT is one of the most famous examples, changing the perception of the possibilities of AI even outside the research community. However, besides the impressive performance, the quadratic time and space complexity of Transformers with respect to sequence length pose significant limitations for handling long sequences. While efficient Transformer architectures like Linformer and Performer with linear complexity have emerged as promising solutions, their theoretical understanding remains limited. In this paper, we introduce Sumformer, a novel and simple architecture capable of universally approximating equivariant sequence-to-sequence functions. We use Sumformer to give the first universal approximation results for Linformer and Performer. Moreover, we derive a new proof for Transformers, showing that just one attention layer is sufficient for universal approximation.