PAC-Bayes Compression Bounds So Tight That They Can Explain Generalization
Paper and Code
Nov 24, 2022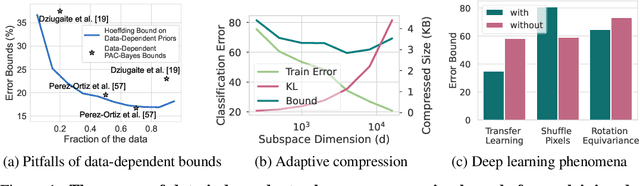

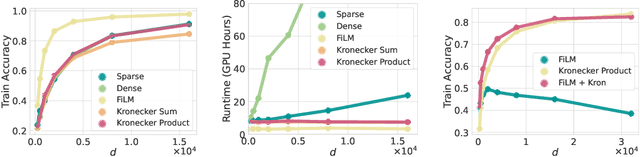
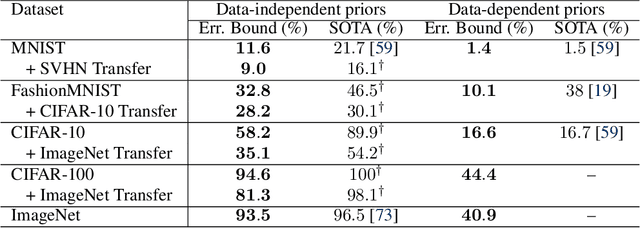
While there has been progress in developing non-vacuous generalization bounds for deep neural networks, these bounds tend to be uninformative about why deep learning works. In this paper, we develop a compression approach based on quantizing neural network parameters in a linear subspace, profoundly improving on previous results to provide state-of-the-art generalization bounds on a variety of tasks, including transfer learning. We use these tight bounds to better understand the role of model size, equivariance, and the implicit biases of optimization, for generalization in deep learning. Notably, we find large models can be compressed to a much greater extent than previously known, encapsulating Occam's razor. We also argue for data-independent bounds in explaining generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge