On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification
Paper and Code
Mar 30, 2022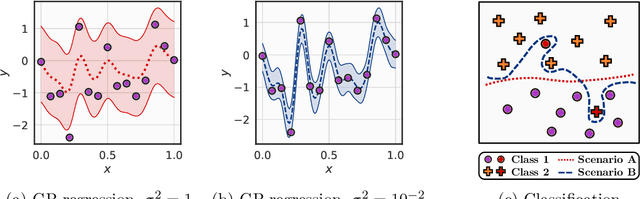
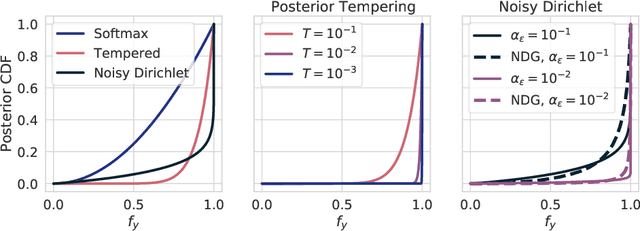
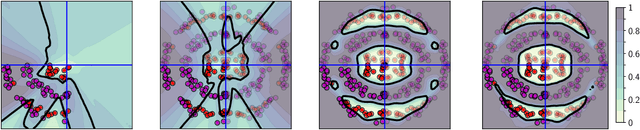
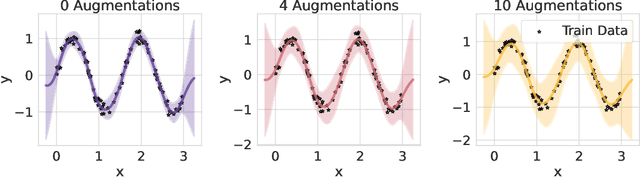
Aleatoric uncertainty captures the inherent randomness of the data, such as measurement noise. In Bayesian regression, we often use a Gaussian observation model, where we control the level of aleatoric uncertainty with a noise variance parameter. By contrast, for Bayesian classification we use a categorical distribution with no mechanism to represent our beliefs about aleatoric uncertainty. Our work shows that explicitly accounting for aleatoric uncertainty significantly improves the performance of Bayesian neural networks. We note that many standard benchmarks, such as CIFAR, have essentially no aleatoric uncertainty. Moreover, we show data augmentation in approximate inference has the effect of softening the likelihood, leading to underconfidence and profoundly misrepresenting our honest beliefs about aleatoric uncertainty. Accordingly, we find that a cold posterior, tempered by a power greater than one, often more honestly reflects our beliefs about aleatoric uncertainty than no tempering -- providing an explicit link between data augmentation and cold posteriors. We show that we can match or exceed the performance of posterior tempering by using a Dirichlet observation model, where we explicitly control the level of aleatoric uncertainty, without any need for tempering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge