Adel Nikfarjam
Evolutionary Diversity Optimisation in Constructing Satisfying Assignments
May 19, 2023



Abstract:Computing diverse solutions for a given problem, in particular evolutionary diversity optimisation (EDO), is a hot research topic in the evolutionary computation community. This paper studies the Boolean satisfiability problem (SAT) in the context of EDO. SAT is of great importance in computer science and differs from the other problems studied in EDO literature, such as KP and TSP. SAT is heavily constrained, and the conventional evolutionary operators are inefficient in generating SAT solutions. Our approach avails of the following characteristics of SAT: 1) the possibility of adding more constraints (clauses) to the problem to forbid solutions or to fix variables, and 2) powerful solvers in the literature, such as minisat. We utilise such a solver to construct a diverse set of solutions. Moreover, maximising diversity provides us with invaluable information about the solution space of a given SAT problem, such as how large the feasible region is. In this study, we introduce evolutionary algorithms (EAs) employing a well-known SAT solver to maximise diversity among a set of SAT solutions explicitly. The experimental investigations indicate the introduced algorithms' capability to maximise diversity among the SAT solutions.
Computing High-Quality Solutions for the Patient Admission Scheduling Problem using Evolutionary Diversity Optimisation
Jul 28, 2022



Abstract:Diversification in a set of solutions has become a hot research topic in the evolutionary computation community. It has been proven beneficial for optimisation problems in several ways, such as computing a diverse set of high-quality solutions and obtaining robustness against imperfect modeling. For the first time in the literature, we adapt the evolutionary diversity optimisation for a real-world combinatorial problem, namely patient admission scheduling. We introduce an evolutionary algorithm to achieve structural diversity in a set of solutions subjected to the quality of each solution. We also introduce a mutation operator biased towards diversity maximisation. Finally, we demonstrate the importance of diversity for the aforementioned problem through a simulation.
Analysis of Quality Diversity Algorithms for the Knapsack Problem
Jul 28, 2022



Abstract:Quality diversity (QD) algorithms have been shown to be very successful when dealing with problems in areas such as robotics, games and combinatorial optimization. They aim to maximize the quality of solutions for different regions of the so-called behavioural space of the underlying problem. In this paper, we apply the QD paradigm to simulate dynamic programming behaviours on knapsack problem, and provide a first runtime analysis of QD algorithms. We show that they are able to compute an optimal solution within expected pseudo-polynomial time, and reveal parameter settings that lead to a fully polynomial randomised approximation scheme (FPRAS). Our experimental investigations evaluate the different approaches on classical benchmark sets in terms of solutions constructed in the behavioural space as well as the runtime needed to obtain an optimal solution.
Co-Evolutionary Diversity Optimisation for the Traveling Thief Problem
Jul 28, 2022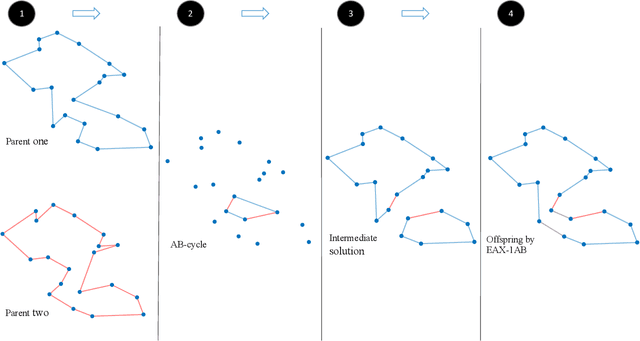



Abstract:Recently different evolutionary computation approaches have been developed that generate sets of high quality diverse solutions for a given optimisation problem. Many studies have considered diversity 1) as a mean to explore niches in behavioural space (quality diversity) or 2) to increase the structural differences of solutions (evolutionary diversity optimisation). In this study, we introduce a co-evolutionary algorithm to simultaneously explore the two spaces for the multi-component traveling thief problem. The results show the capability of the co-evolutionary algorithm to achieve significantly higher diversity compared to the baseline evolutionary diversity algorithms from the the literature.
Evolutionary Diversity Optimisation for The Traveling Thief Problem
Apr 06, 2022



Abstract:There has been a growing interest in the evolutionary computation community to compute a diverse set of high-quality solutions for a given optimisation problem. This can provide the practitioners with invaluable information about the solution space and robustness against imperfect modelling and minor problems' changes. It also enables the decision-makers to involve their interests and choose between various solutions. In this study, we investigate for the first time a prominent multi-component optimisation problem, namely the Traveling Thief Problem (TTP), in the context of evolutionary diversity optimisation. We introduce a bi-level evolutionary algorithm to maximise the structural diversity of the set of solutions. Moreover, we examine the inter-dependency among the components of the problem in terms of structural diversity and empirically determine the best method to obtain diversity. We also conduct a comprehensive experimental investigation to examine the introduced algorithm and compare the results to another recently introduced framework based on the use of Quality Diversity (QD). Our experimental results show a significant improvement of the QD approach in terms of structural diversity for most TTP benchmark instances.
On the Use of Quality Diversity Algorithms for The Traveling Thief Problem
Dec 16, 2021



Abstract:In real-world optimisation, it is common to face several sub-problems interacting and forming the main problem. There is an inter-dependency between the sub-problems, making it impossible to solve such a problem by focusing on only one component. The traveling thief problem~(TTP) belongs to this category and is formed by the integration of the traveling salesperson problem~(TSP) and the knapsack problem~(KP). In this paper, we investigate the inter-dependency of the TSP and the KP by means of quality diversity~(QD) approaches. QD algorithms provide a powerful tool not only to obtain high-quality solutions but also to illustrate the distribution of high-performing solutions in the behavioural space. We introduce a MAP-Elite based evolutionary algorithm using well-known TSP and KP search operators, taking the TSP and KP score as behavioural descriptor. Afterwards, we conduct comprehensive experimental studies that show the usefulness of using the QD approach applied to the TTP. First, we provide insights regarding high-quality TTP solutions in the TSP/KP behavioural space. Afterwards, we show that better solutions for the TTP can be obtained by using our QD approach and show that it can improve the best-known solution for a wide range of TTP instances used for benchmarking in the literature.
Computing Diverse Sets of High Quality TSP Tours by EAX-Based Evolutionary Diversity Optimisation
Aug 12, 2021



Abstract:Evolutionary algorithms based on edge assembly crossover (EAX) constitute some of the best performing incomplete solvers for the well-known traveling salesperson problem (TSP). Often, it is desirable to compute not just a single solution for a given problem, but a diverse set of high quality solutions from which a decision maker can choose one for implementation. Currently, there are only a few approaches for computing a diverse solution set for the TSP. Furthermore, almost all of them assume that the optimal solution is known. In this paper, we introduce evolutionary diversity optimisation (EDO) approaches for the TSP that find a diverse set of tours when the optimal tour is known or unknown. We show how to adopt EAX to not only find a high-quality solution but also to maximise the diversity of the population. The resulting EAX-based EDO approach, termed EAX-EDO is capable of obtaining diverse high-quality tours when the optimal solution for the TSP is known or unknown. A comparison to existing approaches shows that they are clearly outperformed by EAX-EDO.
Entropy-Based Evolutionary Diversity Optimisation for the Traveling Salesperson Problem
Apr 28, 2021



Abstract:Computing diverse sets of high-quality solutions has gained increasing attention among the evolutionary computation community in recent years. It allows practitioners to choose from a set of high-quality alternatives. In this paper, we employ a population diversity measure, called the high-order entropy measure, in an evolutionary algorithm to compute a diverse set of high-quality solutions for the Traveling Salesperson Problem. In contrast to previous studies, our approach allows diversifying segments of tours containing several edges based on the entropy measure. We examine the resulting evolutionary diversity optimisation approach precisely in terms of the final set of solutions and theoretical properties. Experimental results show significant improvements compared to a recently proposed edge-based diversity optimisation approach when working with a large population of solutions or long segments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge