Weighted Embeddings for Low-Dimensional Graph Representation

Learning low-dimensional numerical representations from symbolic data, e.g., embedding the nodes of a graph into a geometric space, is an important concept in machine learning. While embedding into Euclidean space is common, recent observations indicate that hyperbolic geometry is better suited to represent hierarchical information and heterogeneous data (e.g., graphs with a scale-free degree distribution). Despite their potential for more accurate representations, hyperbolic embeddings also have downsides like being more difficult to compute and harder to use in downstream tasks. We propose embedding into a weighted space, which is closely related to hyperbolic geometry but mathematically simpler. We provide the embedding algorithm WEmbed and demonstrate, based on generated as well as over 2000 real-world graphs, that our weighted embeddings heavily outperform state-of-the-art Euclidean embeddings for heterogeneous graphs while using fewer dimensions. The running time of WEmbed and embedding quality for the remaining instances is on par with state-of-the-art Euclidean embedders.

Deep Distance Sensitivity Oracles

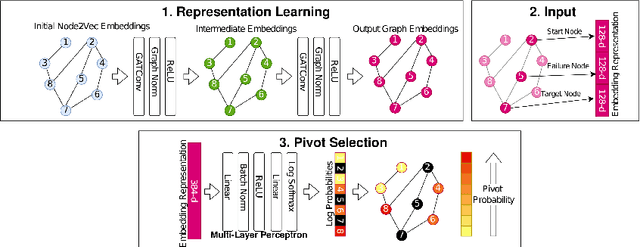
One of the most fundamental graph problems is finding a shortest path from a source to a target node. While in its basic forms the problem has been studied extensively and efficient algorithms are known, it becomes significantly harder as soon as parts of the graph are susceptible to failure. Although one can recompute a shortest replacement path after every outage, this is rather inefficient both in time and/or storage. One way to overcome this problem is to shift computational burden from the queries into a pre-processing step, where a data structure is computed that allows for fast querying of replacement paths, typically referred to as a Distance Sensitivity Oracle (DSO). While DSOs have been extensively studied in the theoretical computer science community, to the best of our knowledge this is the first work to construct DSOs using deep learning techniques. We show how to use deep learning to utilize a combinatorial structure of replacement paths. More specifically, we utilize the combinatorial structure of replacement paths as a concatenation of shortest paths and use deep learning to find the pivot nodes for stitching shortest paths into replacement paths.

Towards Explainable Real Estate Valuation via Evolutionary Algorithms

Human lives are increasingly influenced by algorithms, which therefore need to meet higher standards not only in accuracy but also with respect to explainability. This is especially true for high-stakes areas such as real estate valuation, where algorithms decide over the price of one of the most valuable objects one can own. Unfortunately, the methods applied there often exhibit a trade-off between accuracy and explainability. On the one hand, there are explainable approaches such as case-based reasoning (CBR), where each decision is supported by specific previous cases. However, such methods are often wanting in accuracy. On the other hand, there are unexplainable machine learning approaches, which provide higher accuracy but are not scrutable in their decision-making. In this paper, we apply evolutionary algorithms (EAs) to close the performance gap between explainable and unexplainable approaches. They yield similarity functions (used in CBR to find comparable cases), which are fitted to the data set at hand. As a consequence, CBR achieves higher accuracy than state-of-the-art deep neural networks (DNNs), while maintaining its interpretability and explainability. This holds true even when we fit the neural network architecture to the data using evolutionary architecture search. These results stem from our empirical evaluation on a large data set of real estate offers from Japan, where we compare known similarity functions and DNN architectures with their EA-improved counterparts. In our testing, DNNs outperform previous CBR approaches. However, with the EA-learned similarity function CBR is even more accurate than DNNs.

A Practical Maximum Clique Algorithm for Matching with Pairwise Constraints

A popular paradigm for 3D point cloud registration is by extracting 3D keypoint correspondences, then estimating the registration function from the correspondences using a robust algorithm. However, many existing 3D keypoint techniques tend to produce large proportions of erroneous correspondences or outliers, which significantly increases the cost of robust estimation. An alternative approach is to directly search for the subset of correspondences that are pairwise consistent, without optimising the registration function. This gives rise to the combinatorial problem of matching with pairwise constraints. In this paper, we propose a very efficient maximum clique algorithm to solve matching with pairwise constraints. Our technique combines tree searching with efficient bounding and pruning based on graph colouring. We demonstrate that, despite the theoretical intractability, many real problem instances can be solved exactly and quickly (seconds to minutes) with our algorithm, which makes our approach an excellent alternative to standard robust techniques for 3D registration.