Schelling Games with Continuous Types

In most major cities and urban areas, residents form homogeneous neighborhoods along ethnic or socioeconomic lines. This phenomenon is widely known as residential segregation and has been studied extensively. Fifty years ago, Schelling proposed a landmark model that explains residential segregation in an elegant agent-based way. A recent stream of papers analyzed Schelling's model using game-theoretic approaches. However, all these works considered models with a given number of discrete types modeling different ethnic groups. We focus on segregation caused by non-categorical attributes, such as household income or position in a political left-right spectrum. For this, we consider agent types that can be represented as real numbers. This opens up a great variety of reasonable models and, as a proof of concept, we focus on several natural candidates. In particular, we consider agents that evaluate their location by the average type-difference or the maximum type-difference to their neighbors, or by having a certain tolerance range for type-values of neighboring agents. We study the existence and computation of equilibria and provide bounds on the Price of Anarchy and Stability. Also, we present simulation results that compare our models and shed light on the obtained equilibria for our variants.

Single-Peaked Jump Schelling Games

Schelling games model the wide-spread phenomenon of residential segregation in metropolitan areas from a game-theoretic point of view. In these games agents of different types each strategically select a node on a given graph that models the residential area to maximize their individual utility. The latter solely depends on the types of the agents on neighboring nodes and it has been a standard assumption to consider utility functions that are monotone in the number of same-type neighbors. This simplifying assumption has recently been challenged since sociological poll results suggest that real-world agents actually favor diverse neighborhoods. We contribute to the recent endeavor of investigating residential segregation models with realistic agent behavior by studying Jump Schelling Games with agents having a single-peaked utility function. In such games, there are empty nodes in the graph and agents can strategically jump to such nodes to improve their utility. We investigate the existence of equilibria and show that they exist under specific conditions. Contrasting this, we prove that even on simple topologies like paths or rings such stable states are not guaranteed to exist. Regarding the game dynamics, we show that improving response cycles exist independently of the position of the peak in the utility function. Moreover, we show high almost tight bounds on the Price of Anarchy and the Price of Stability with respect to the recently proposed degree of integration, which counts the number of agents with a diverse neighborhood and which serves as a proxy for measuring the segregation strength. Last but not least, we show that computing a beneficial state with high integration is NP-complete and, as a novel conceptual contribution, we also show that it is NP-hard to decide if an equilibrium state can be found via improving response dynamics starting from a given initial state.

Towards Explainable Real Estate Valuation via Evolutionary Algorithms

Human lives are increasingly influenced by algorithms, which therefore need to meet higher standards not only in accuracy but also with respect to explainability. This is especially true for high-stakes areas such as real estate valuation, where algorithms decide over the price of one of the most valuable objects one can own. Unfortunately, the methods applied there often exhibit a trade-off between accuracy and explainability. On the one hand, there are explainable approaches such as case-based reasoning (CBR), where each decision is supported by specific previous cases. However, such methods are often wanting in accuracy. On the other hand, there are unexplainable machine learning approaches, which provide higher accuracy but are not scrutable in their decision-making. In this paper, we apply evolutionary algorithms (EAs) to close the performance gap between explainable and unexplainable approaches. They yield similarity functions (used in CBR to find comparable cases), which are fitted to the data set at hand. As a consequence, CBR achieves higher accuracy than state-of-the-art deep neural networks (DNNs), while maintaining its interpretability and explainability. This holds true even when we fit the neural network architecture to the data using evolutionary architecture search. These results stem from our empirical evaluation on a large data set of real estate offers from Japan, where we compare known similarity functions and DNN architectures with their EA-improved counterparts. In our testing, DNNs outperform previous CBR approaches. However, with the EA-learned similarity function CBR is even more accurate than DNNs.

Two-Stage Facility Location Games with Strategic Clients and Facilities

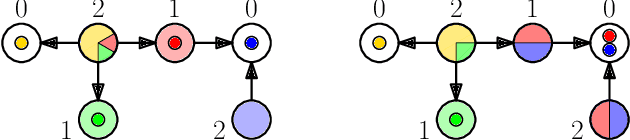
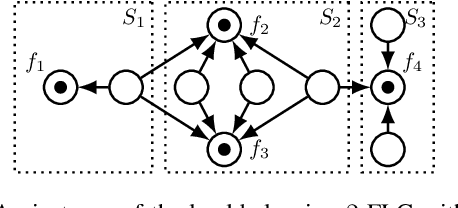
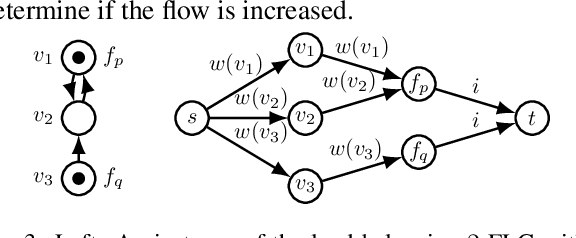
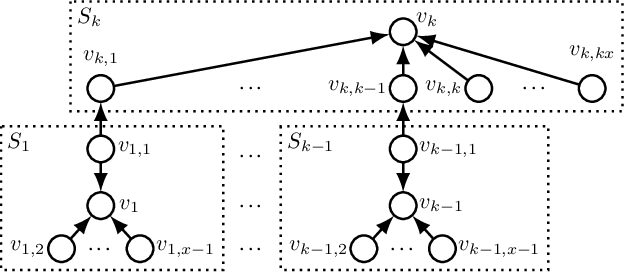
We consider non-cooperative facility location games where both facilities and clients act strategically and heavily influence each other. This contrasts established game-theoretic facility location models with non-strategic clients that simply select the closest opened facility. In our model, every facility location has a set of attracted clients and each client has a set of shopping locations and a weight that corresponds to her spending capacity. Facility agents selfishly select a location for opening their facility to maximize the attracted total spending capacity, whereas clients strategically decide how to distribute their spending capacity among the opened facilities in their shopping range. We focus on a natural client behavior similar to classical load balancing: our selfish clients aim for a distribution that minimizes their maximum waiting times for getting serviced, where a facility's waiting time corresponds to its total attracted client weight. We show that subgame perfect equilibria exist and give almost tight constant bounds on the Price of Anarchy and the Price of Stability, which even hold for a broader class of games with arbitrary client behavior. Since facilities and clients influence each other, it is crucial for the facilities to anticipate the selfish clients' behavior when selecting their location. For this, we provide an efficient algorithm that also implies an efficient check for equilibrium. Finally, we show that computing a socially optimal facility placement is NP-hard and that this result holds for all feasible client weight distributions.