Two-Stage Facility Location Games with Strategic Clients and Facilities
Paper and Code
May 04, 2021
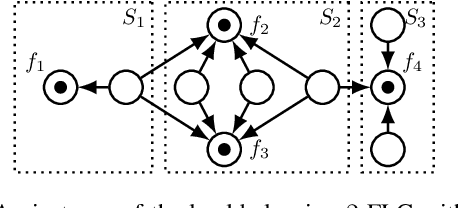
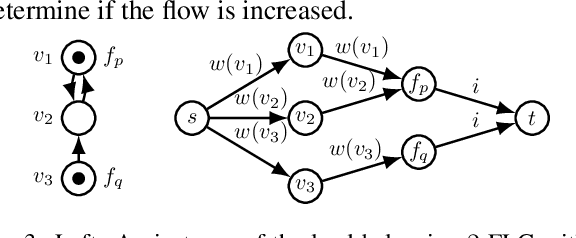
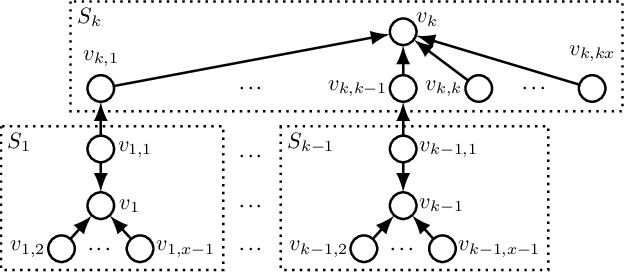
We consider non-cooperative facility location games where both facilities and clients act strategically and heavily influence each other. This contrasts established game-theoretic facility location models with non-strategic clients that simply select the closest opened facility. In our model, every facility location has a set of attracted clients and each client has a set of shopping locations and a weight that corresponds to her spending capacity. Facility agents selfishly select a location for opening their facility to maximize the attracted total spending capacity, whereas clients strategically decide how to distribute their spending capacity among the opened facilities in their shopping range. We focus on a natural client behavior similar to classical load balancing: our selfish clients aim for a distribution that minimizes their maximum waiting times for getting serviced, where a facility's waiting time corresponds to its total attracted client weight. We show that subgame perfect equilibria exist and give almost tight constant bounds on the Price of Anarchy and the Price of Stability, which even hold for a broader class of games with arbitrary client behavior. Since facilities and clients influence each other, it is crucial for the facilities to anticipate the selfish clients' behavior when selecting their location. For this, we provide an efficient algorithm that also implies an efficient check for equilibrium. Finally, we show that computing a socially optimal facility placement is NP-hard and that this result holds for all feasible client weight distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge