The Bakers and Millers Game with Restricted Locations

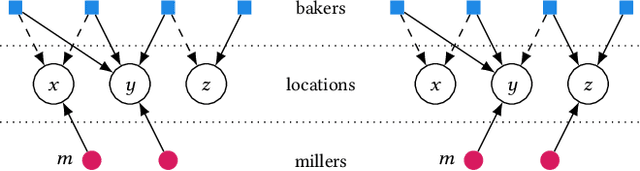
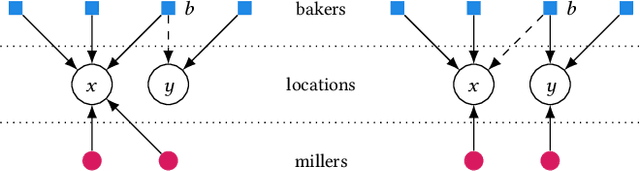
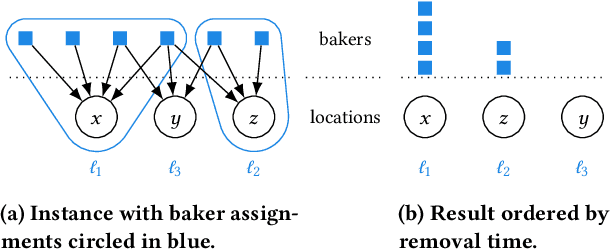
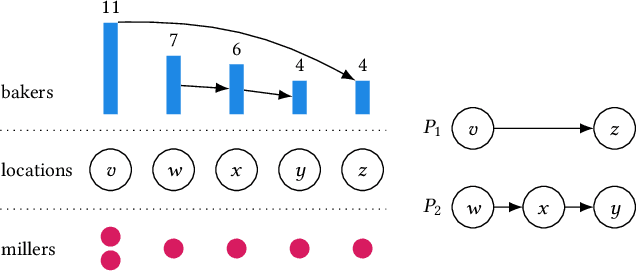
We study strategic location choice by customers and sellers, termed the Bakers and Millers Game in the literature. In our generalized setting, each miller can freely choose any location for setting up a mill, while each baker is restricted in the choice of location for setting up a bakery. For optimal bargaining power, a baker would like to select a location with many millers to buy flour from and with little competition from other bakers. Likewise, a miller aims for a location with many bakers and few competing millers. Thus, both types of agents choose locations to optimize the ratio of agents of opposite type divided by agents of the same type at their chosen location. Originally raised in the context of Fractional Hedonic Games, the Bakers and Millers Game has applications that range from commerce to product design. We study the impact of location restrictions on the properties of the game. While pure Nash equilibria trivially exist in the setting without location restrictions, we show via a sophisticated, efficient algorithm that even the more challenging restricted setting admits equilibria. Moreover, the computed equilibrium approximates the optimal social welfare by a factor of at most $2\left(\frac{e}{e-1}\right)$. Furthermore, we give tight bounds on the price of anarchy/stability. On the conceptual side, the location choice feature adds a new layer to the standard setting of Hedonic Games, in the sense that agents that select the same location form a coalition. This allows to naturally restrict the possible coalitions that can be formed. With this, our model generalizes simple symmetric Fractional Hedonic Games on complete bipartite valuation graphs and also Hedonic Diversity Games with utilities single-peaked at 0. We believe that this generalization is also a very interesting direction for other types of Hedonic Games.

Equilibria in Two-Stage Facility Location with Atomic Clients

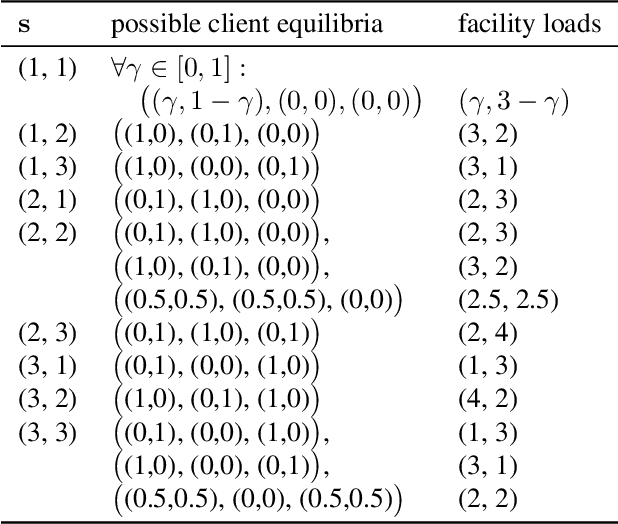
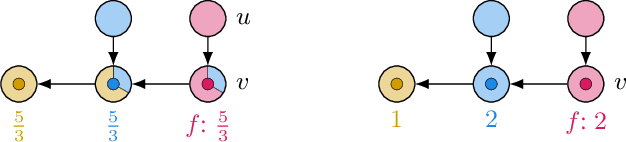
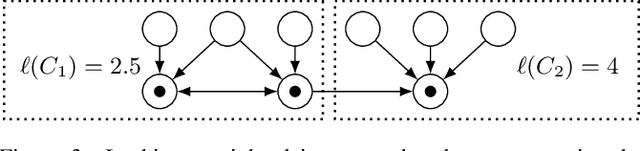
We consider competitive facility location as a two-stage multi-agent system with two types of clients. For a given host graph with weighted clients on the vertices, first facility agents strategically select vertices for opening their facilities. Then, the clients strategically select which of the opened facilities in their neighborhood to patronize. Facilities want to attract as much client weight as possible, clients want to minimize congestion on the chosen facility. All recently studied versions of this model assume that clients can split their weight strategically. We consider clients with unsplittable weights, but allow mixed strategies. So clients may randomize over which facility to patronize. Besides modeling a natural client behavior, this subtle change yields drastic changes, e.g., for a given facility placement, qualitatively different client equilibria are possible. As our main result, we show that pure subgame perfect equilibria always exist if all client weights are identical. For this, we use a novel potential function argument, employing a hierarchical classification of the clients and sophisticated rounding in each step. In contrast, for non-identical clients, we show that deciding the existence of even approximately stable states is computationally intractable. On the positive side, we give a tight bound of 2 on the price of anarchy which implies high social welfare of equilibria, if they exist.

Temporal Network Creation Games

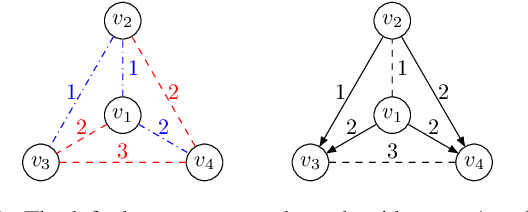
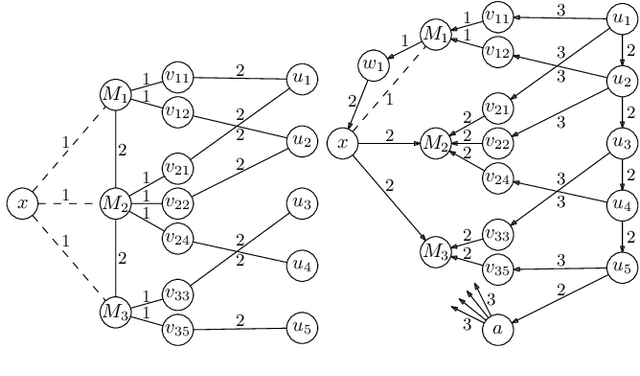
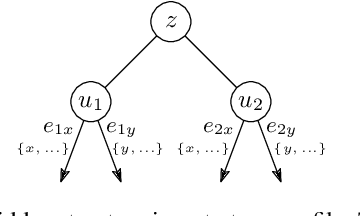
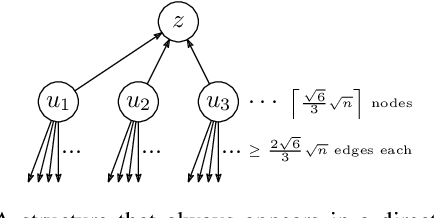
Most networks are not static objects, but instead they change over time. This observation has sparked rigorous research on temporal graphs within the last years. In temporal graphs, we have a fixed set of nodes and the connections between them are only available at certain time steps. This gives rise to a plethora of algorithmic problems on such graphs, most prominently the problem of finding temporal spanners, i.e., the computation of subgraphs that guarantee all pairs reachability via temporal paths. To the best of our knowledge, only centralized approaches for the solution of this problem are known. However, many real-world networks are not shaped by a central designer but instead they emerge and evolve by the interaction of many strategic agents. This observation is the driving force of the recent intensive research on game-theoretic network formation models. In this work we bring together these two recent research directions: temporal graphs and game-theoretic network formation. As a first step into this new realm, we focus on a simplified setting where a complete temporal host graph is given and the agents, corresponding to its nodes, selfishly create incident edges to ensure that they can reach all other nodes via temporal paths in the created network. This yields temporal spanners as equilibria of our game. We prove results on the convergence to and the existence of equilibrium networks, on the complexity of finding best agent strategies, and on the quality of the equilibria. By taking these first important steps, we uncover challenging open problems that call for an in-depth exploration of the creation of temporal graphs by strategic agents.

Schelling Games with Continuous Types

In most major cities and urban areas, residents form homogeneous neighborhoods along ethnic or socioeconomic lines. This phenomenon is widely known as residential segregation and has been studied extensively. Fifty years ago, Schelling proposed a landmark model that explains residential segregation in an elegant agent-based way. A recent stream of papers analyzed Schelling's model using game-theoretic approaches. However, all these works considered models with a given number of discrete types modeling different ethnic groups. We focus on segregation caused by non-categorical attributes, such as household income or position in a political left-right spectrum. For this, we consider agent types that can be represented as real numbers. This opens up a great variety of reasonable models and, as a proof of concept, we focus on several natural candidates. In particular, we consider agents that evaluate their location by the average type-difference or the maximum type-difference to their neighbors, or by having a certain tolerance range for type-values of neighboring agents. We study the existence and computation of equilibria and provide bounds on the Price of Anarchy and Stability. Also, we present simulation results that compare our models and shed light on the obtained equilibria for our variants.

Strategic Resource Selection with Homophilic Agents

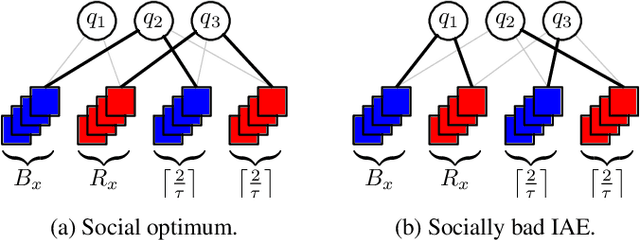
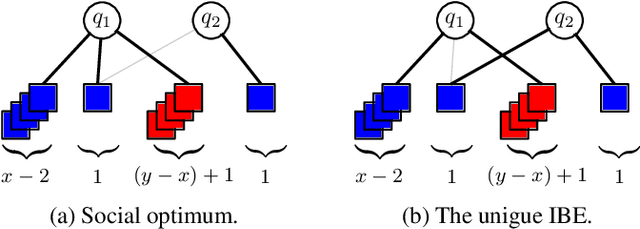
The strategic selection of resources by selfish agents is a classic research direction, with Resource Selection Games and Congestion Games as prominent examples. In these games, agents select available resources and their utility then depends on the number of agents using the same resources. This implies that there is no distinction between the agents, i.e., they are anonymous. We depart from this very general setting by proposing Resource Selection Games with heterogeneous agents that strive for joint resource usage with similar agents. So, instead of the number of other users of a given resource, our model considers agents with different types and the decisive feature is the fraction of same-type agents among the users. More precisely, similarly to Schelling Games, there is a tolerance threshold $\tau \in [0,1]$ which specifies the agents' desired minimum fraction of same-type agents on a resource. Agents strive to select resources where at least a $\tau$-fraction of those resources' users have the same type as themselves. For $\tau=1$, our model generalizes Hedonic Diversity Games with a peak at $1$. For our general model, we consider the existence and quality of equilibria and the complexity of maximizing social welfare. Additionally, we consider a bounded rationality model, where agents can only estimate the utility of a resource, since they only know the fraction of same-type agents on a given resource, but not the exact numbers. Thus, they cannot know the impact a strategy change would have on a target resource. Interestingly, we show that this type of bounded rationality yields favorable game-theoretic properties and specific equilibria closely approximate equilibria of the full knowledge setting.

Single-Peaked Jump Schelling Games

Schelling games model the wide-spread phenomenon of residential segregation in metropolitan areas from a game-theoretic point of view. In these games agents of different types each strategically select a node on a given graph that models the residential area to maximize their individual utility. The latter solely depends on the types of the agents on neighboring nodes and it has been a standard assumption to consider utility functions that are monotone in the number of same-type neighbors. This simplifying assumption has recently been challenged since sociological poll results suggest that real-world agents actually favor diverse neighborhoods. We contribute to the recent endeavor of investigating residential segregation models with realistic agent behavior by studying Jump Schelling Games with agents having a single-peaked utility function. In such games, there are empty nodes in the graph and agents can strategically jump to such nodes to improve their utility. We investigate the existence of equilibria and show that they exist under specific conditions. Contrasting this, we prove that even on simple topologies like paths or rings such stable states are not guaranteed to exist. Regarding the game dynamics, we show that improving response cycles exist independently of the position of the peak in the utility function. Moreover, we show high almost tight bounds on the Price of Anarchy and the Price of Stability with respect to the recently proposed degree of integration, which counts the number of agents with a diverse neighborhood and which serves as a proxy for measuring the segregation strength. Last but not least, we show that computing a beneficial state with high integration is NP-complete and, as a novel conceptual contribution, we also show that it is NP-hard to decide if an equilibrium state can be found via improving response dynamics starting from a given initial state.

Strategic Facility Location with Clients that Minimize Total Waiting Time

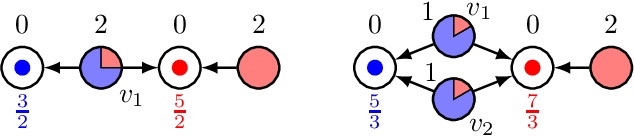
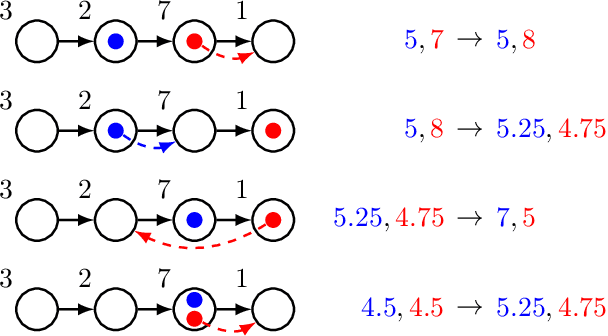
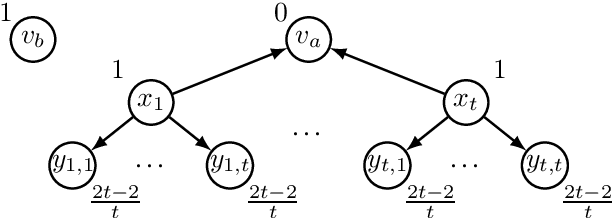
We study a non-cooperative two-sided facility location game in which facilities and clients behave strategically. This is in contrast to many other facility location games in which clients simply visit their closest facility. Facility agents select a location on a graph to open a facility to attract as much purchasing power as possible, while client agents choose which facilities to patronize by strategically distributing their purchasing power in order to minimize their total waiting time. Here, the waiting time of a facility depends on its received total purchasing power. We show that our client stage is an atomic splittable congestion game, which implies existence, uniqueness and efficient computation of a client equilibrium. Therefore, facility agents can efficiently predict client behavior and make strategic decisions accordingly. Despite that, we prove that subgame perfect equilibria do not exist in all instances of this game and that their existence is NP-hard to decide. On the positive side, we provide a simple and efficient algorithm to compute 3-approximate subgame perfect equilibria.

Two-Stage Facility Location Games with Strategic Clients and Facilities

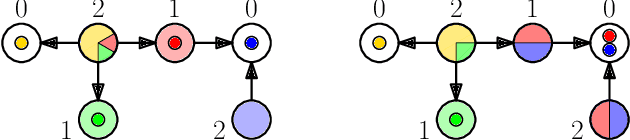
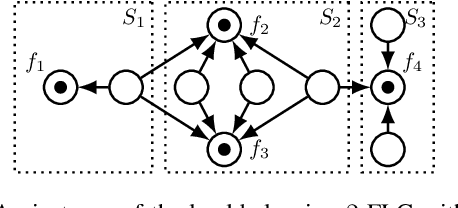
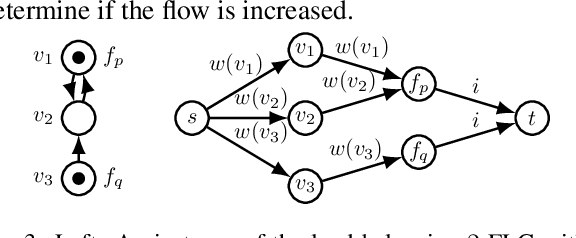
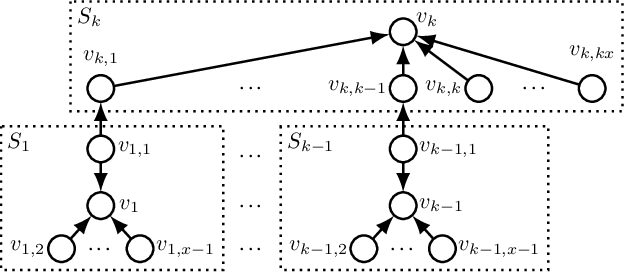
We consider non-cooperative facility location games where both facilities and clients act strategically and heavily influence each other. This contrasts established game-theoretic facility location models with non-strategic clients that simply select the closest opened facility. In our model, every facility location has a set of attracted clients and each client has a set of shopping locations and a weight that corresponds to her spending capacity. Facility agents selfishly select a location for opening their facility to maximize the attracted total spending capacity, whereas clients strategically decide how to distribute their spending capacity among the opened facilities in their shopping range. We focus on a natural client behavior similar to classical load balancing: our selfish clients aim for a distribution that minimizes their maximum waiting times for getting serviced, where a facility's waiting time corresponds to its total attracted client weight. We show that subgame perfect equilibria exist and give almost tight constant bounds on the Price of Anarchy and the Price of Stability, which even hold for a broader class of games with arbitrary client behavior. Since facilities and clients influence each other, it is crucial for the facilities to anticipate the selfish clients' behavior when selecting their location. For this, we provide an efficient algorithm that also implies an efficient check for equilibrium. Finally, we show that computing a socially optimal facility placement is NP-hard and that this result holds for all feasible client weight distributions.