The Bakers and Millers Game with Restricted Locations
Paper and Code
Jan 09, 2025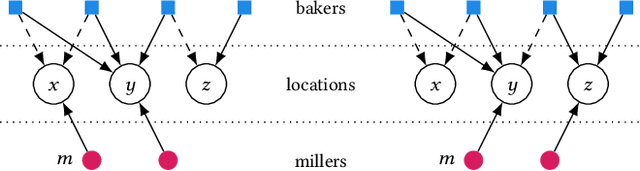
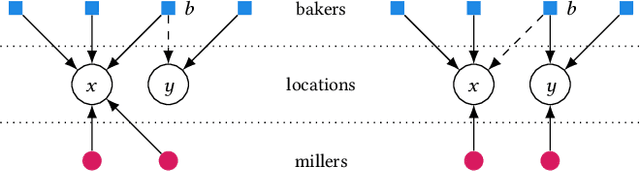
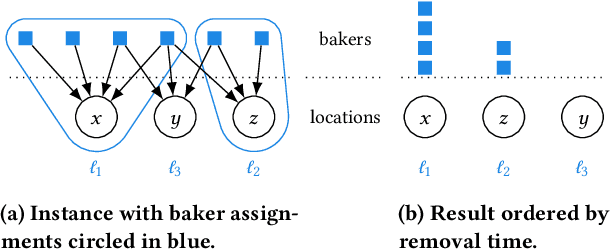
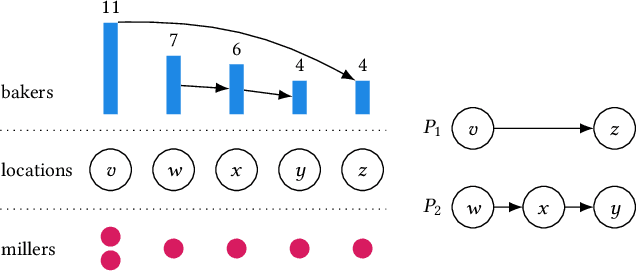
We study strategic location choice by customers and sellers, termed the Bakers and Millers Game in the literature. In our generalized setting, each miller can freely choose any location for setting up a mill, while each baker is restricted in the choice of location for setting up a bakery. For optimal bargaining power, a baker would like to select a location with many millers to buy flour from and with little competition from other bakers. Likewise, a miller aims for a location with many bakers and few competing millers. Thus, both types of agents choose locations to optimize the ratio of agents of opposite type divided by agents of the same type at their chosen location. Originally raised in the context of Fractional Hedonic Games, the Bakers and Millers Game has applications that range from commerce to product design. We study the impact of location restrictions on the properties of the game. While pure Nash equilibria trivially exist in the setting without location restrictions, we show via a sophisticated, efficient algorithm that even the more challenging restricted setting admits equilibria. Moreover, the computed equilibrium approximates the optimal social welfare by a factor of at most $2\left(\frac{e}{e-1}\right)$. Furthermore, we give tight bounds on the price of anarchy/stability. On the conceptual side, the location choice feature adds a new layer to the standard setting of Hedonic Games, in the sense that agents that select the same location form a coalition. This allows to naturally restrict the possible coalitions that can be formed. With this, our model generalizes simple symmetric Fractional Hedonic Games on complete bipartite valuation graphs and also Hedonic Diversity Games with utilities single-peaked at 0. We believe that this generalization is also a very interesting direction for other types of Hedonic Games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge