Analysis of Evolutionary Diversity Optimisation for the Maximum Matching Problem

This paper explores the enhancement of solution diversity in evolutionary algorithms (EAs) for the maximum matching problem, concentrating on complete bipartite graphs and paths. We adopt binary string encoding for matchings and use Hamming distance to measure diversity, aiming for its maximization. Our study centers on the $(\mu+1)$-EA and $2P-EA_D$, which are applied to optimize diversity. We provide a rigorous theoretical and empirical analysis of these algorithms. For complete bipartite graphs, our runtime analysis shows that, with a reasonably small $\mu$, the $(\mu+1)$-EA achieves maximal diversity with an expected runtime of $O(\mu^2 m^4 \log(m))$ for the small gap case (where the population size $\mu$ is less than the difference in the sizes of the bipartite partitions) and $O(\mu^2 m^2 \log(m))$ otherwise. For paths, we establish an upper runtime bound of $O(\mu^3 m^3)$. The $2P-EA_D$ displays stronger performance, with bounds of $O(\mu^2 m^2 \log(m))$ for the small gap case, $O(\mu^2 n^2 \log(n))$ otherwise, and $O(\mu^3 m^2)$ for paths. Here, $n$ represents the total number of vertices and $m$ the number of edges. Our empirical studies, which examine the scaling behavior with respect to $m$ and $\mu$, complement these theoretical insights and suggest potential for further refinement of the runtime bounds.

Run Time Bounds for Integer-Valued OneMax Functions

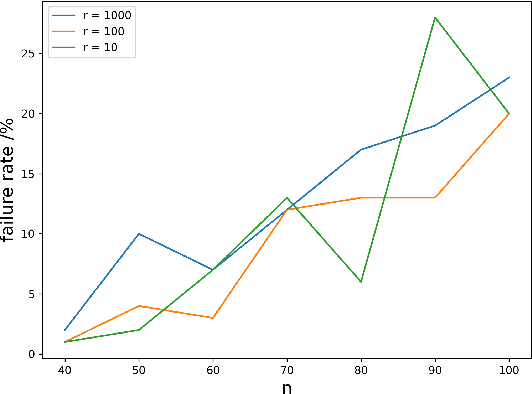
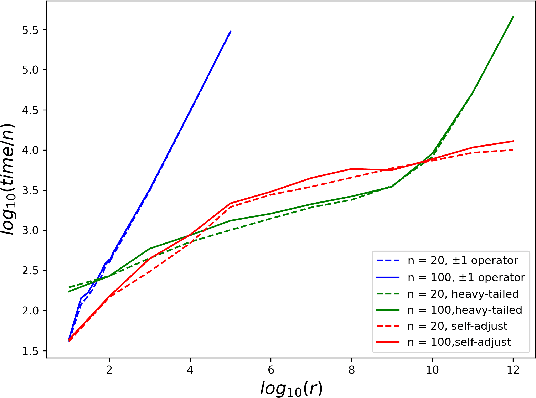
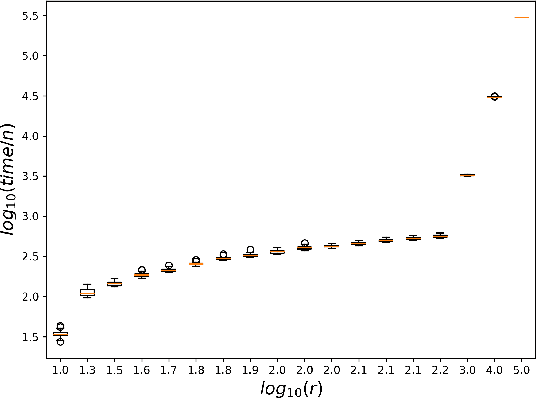
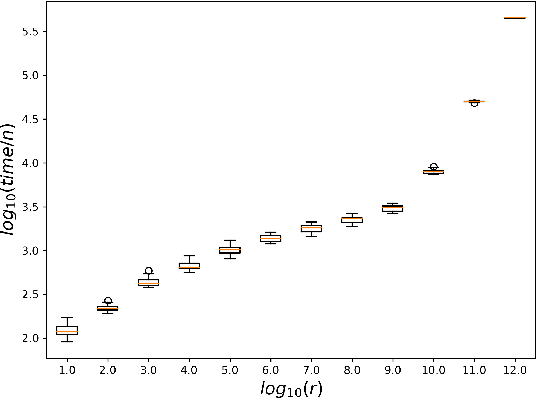
While most theoretical run time analyses of discrete randomized search heuristics focused on finite search spaces, we consider the search space $\mathbb{Z}^n$. This is a further generalization of the search space of multi-valued decision variables $\{0,\ldots,r-1\}^n$. We consider as fitness functions the distance to the (unique) non-zero optimum $a$ (based on the $L_1$-metric) and the \ooea which mutates by applying a step-operator on each component that is determined to be varied. For changing by $\pm 1$, we show that the expected optimization time is $\Theta(n \cdot (|a|_{\infty} + \log(|a|_H)))$. In particular, the time is linear in the maximum value of the optimum $a$. Employing a different step operator which chooses a step size from a distribution so heavy-tailed that the expectation is infinite, we get an optimization time of $O(n \cdot \log^2 (|a|_1) \cdot \left(\log (\log (|a|_1))\right)^{1 + \epsilon})$. Furthermore, we show that RLS with step size adaptation achieves an optimization time of $\Theta(n \cdot \log(|a|_1))$. We conclude with an empirical analysis, comparing the above algorithms also with a variant of CMA-ES for discrete search spaces.

Strategic Resource Selection with Homophilic Agents

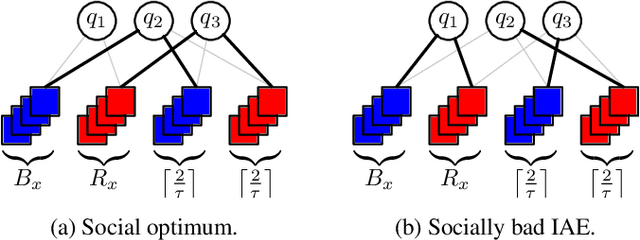
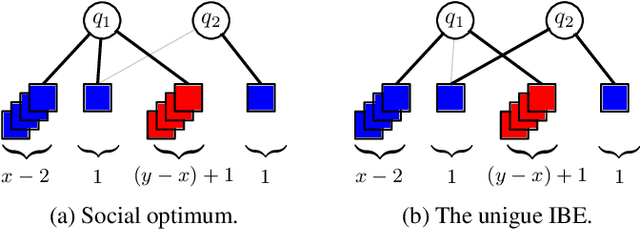
The strategic selection of resources by selfish agents is a classic research direction, with Resource Selection Games and Congestion Games as prominent examples. In these games, agents select available resources and their utility then depends on the number of agents using the same resources. This implies that there is no distinction between the agents, i.e., they are anonymous. We depart from this very general setting by proposing Resource Selection Games with heterogeneous agents that strive for joint resource usage with similar agents. So, instead of the number of other users of a given resource, our model considers agents with different types and the decisive feature is the fraction of same-type agents among the users. More precisely, similarly to Schelling Games, there is a tolerance threshold $\tau \in [0,1]$ which specifies the agents' desired minimum fraction of same-type agents on a resource. Agents strive to select resources where at least a $\tau$-fraction of those resources' users have the same type as themselves. For $\tau=1$, our model generalizes Hedonic Diversity Games with a peak at $1$. For our general model, we consider the existence and quality of equilibria and the complexity of maximizing social welfare. Additionally, we consider a bounded rationality model, where agents can only estimate the utility of a resource, since they only know the fraction of same-type agents on a given resource, but not the exact numbers. Thus, they cannot know the impact a strategy change would have on a target resource. Interestingly, we show that this type of bounded rationality yields favorable game-theoretic properties and specific equilibria closely approximate equilibria of the full knowledge setting.

Maps for Learning Indexable Classes

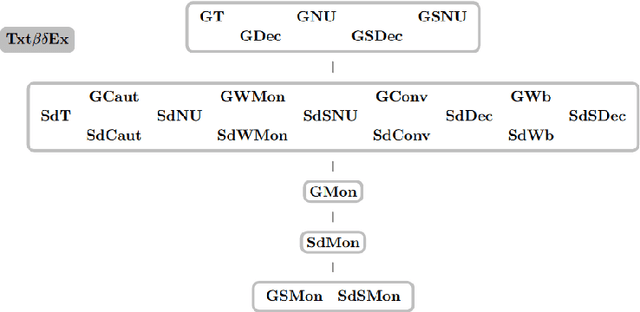
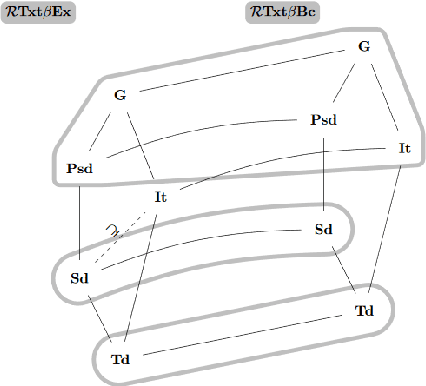
We study learning of indexed families from positive data where a learner can freely choose a hypothesis space (with uniformly decidable membership) comprising at least the languages to be learned. This abstracts a very universal learning task which can be found in many areas, for example learning of (subsets of) regular languages or learning of natural languages. We are interested in various restrictions on learning, such as consistency, conservativeness or set-drivenness, exemplifying various natural learning restrictions. Building on previous results from the literature, we provide several maps (depictions of all pairwise relations) of various groups of learning criteria, including a map for monotonicity restrictions and similar criteria and a map for restrictions on data presentation. Furthermore, we consider, for various learning criteria, whether learners can be assumed consistent.