Towards Explainable Real Estate Valuation via Evolutionary Algorithms

Human lives are increasingly influenced by algorithms, which therefore need to meet higher standards not only in accuracy but also with respect to explainability. This is especially true for high-stakes areas such as real estate valuation, where algorithms decide over the price of one of the most valuable objects one can own. Unfortunately, the methods applied there often exhibit a trade-off between accuracy and explainability. On the one hand, there are explainable approaches such as case-based reasoning (CBR), where each decision is supported by specific previous cases. However, such methods are often wanting in accuracy. On the other hand, there are unexplainable machine learning approaches, which provide higher accuracy but are not scrutable in their decision-making. In this paper, we apply evolutionary algorithms (EAs) to close the performance gap between explainable and unexplainable approaches. They yield similarity functions (used in CBR to find comparable cases), which are fitted to the data set at hand. As a consequence, CBR achieves higher accuracy than state-of-the-art deep neural networks (DNNs), while maintaining its interpretability and explainability. This holds true even when we fit the neural network architecture to the data using evolutionary architecture search. These results stem from our empirical evaluation on a large data set of real estate offers from Japan, where we compare known similarity functions and DNN architectures with their EA-improved counterparts. In our testing, DNNs outperform previous CBR approaches. However, with the EA-learned similarity function CBR is even more accurate than DNNs.

Adaptive Sampling for Fast Constrained Maximization of Submodular Function

Several large-scale machine learning tasks, such as data summarization, can be approached by maximizing functions that satisfy submodularity. These optimization problems often involve complex side constraints, imposed by the underlying application. In this paper, we develop an algorithm with poly-logarithmic adaptivity for non-monotone submodular maximization under general side constraints. The adaptive complexity of a problem is the minimal number of sequential rounds required to achieve the objective. Our algorithm is suitable to maximize a non-monotone submodular function under a $p$-system side constraint, and it achieves a $(p + O(\sqrt{p}))$-approximation for this problem, after only poly-logarithmic adaptive rounds and polynomial queries to the valuation oracle function. Furthermore, our algorithm achieves a $(p + O(1))$-approximation when the given side constraint is a $p$-extendible system. This algorithm yields an exponential speed-up, with respect to the adaptivity, over any other known constant-factor approximation algorithm for this problem. It also competes with previous known results in terms of the query complexity. We perform various experiments on various real-world applications. We find that, in comparison with commonly used heuristics, our algorithm performs better on these instances.

Maps for Learning Indexable Classes

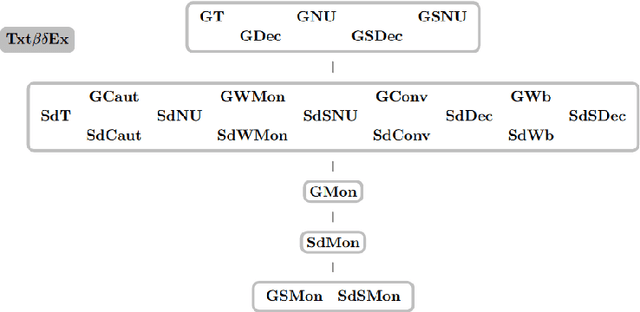
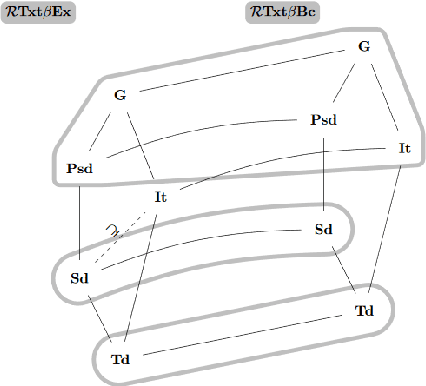
We study learning of indexed families from positive data where a learner can freely choose a hypothesis space (with uniformly decidable membership) comprising at least the languages to be learned. This abstracts a very universal learning task which can be found in many areas, for example learning of (subsets of) regular languages or learning of natural languages. We are interested in various restrictions on learning, such as consistency, conservativeness or set-drivenness, exemplifying various natural learning restrictions. Building on previous results from the literature, we provide several maps (depictions of all pairwise relations) of various groups of learning criteria, including a map for monotonicity restrictions and similar criteria and a map for restrictions on data presentation. Furthermore, we consider, for various learning criteria, whether learners can be assumed consistent.

Normal Forms for Witness-Based Learners in Inductive Inference

We study learners (computable devices) inferring formal languages, a setting referred to as language learning in the limit or inductive inference. In particular, we require the learners we investigate to be witness-based, that is, to justify each of their mind changes. Besides being a natural requirement for a learning task, this restriction deserves special attention as it is a specialization of various important learning paradigms. In particular, with the help of witness-based learning, explanatory learners are shown to be equally powerful under these seemingly incomparable paradigms. Nonetheless, until now, witness-based learners have only been studied sparsely. In this work, we conduct a thorough study of these learners both when requiring syntactic and semantic convergence and obtain normal forms thereof. In the former setting, we extend known results such that they include witness-based learning and generalize these to hold for a variety of learners. Transitioning to behaviourally correct learning, we also provide normal forms for semantically witness-based learners. Most notably, we show that set-driven globally semantically witness-based learners are equally powerful as their Gold-style semantically conservative counterpart. Such results are key to understanding the, yet undiscovered, mutual relation between various important learning paradigms when learning behaviourally correctly.

Mapping Monotonic Restrictions in Inductive Inference

In language learning in the limit we investigate computable devices (learners) learning formal languages. Through the years, many natural restrictions have been imposed on the studied learners. As such, monotonic restrictions always enjoyed particular attention as, although being a natural requirement, monotonic learners show significantly diverse behaviour when studied in different settings. A recent study thoroughly analysed the learning capabilities of strongly monotone learners imposed with memory restrictions and various additional requirements. The unveiled differences between explanatory and behaviourally correct such learners motivate our studies of monotone learners dealing with the same restrictions. We reveal differences and similarities between monotone learners and their strongly monotone counterpart when studied with various additional restrictions. In particular, we show that explanatory monotone learners, although known to be strictly stronger, do (almost) preserve the pairwise relation as seen in strongly monotone learning. Contrasting this similarity, we find substantial differences when studying behaviourally correct monotone learners. Most notably, we show that monotone learners, as opposed to their strongly monotone counterpart, do heavily rely on the order the information is given in, an unusual result for behaviourally correct learners.

timeXplain -- A Framework for Explaining the Predictions of Time Series Classifiers

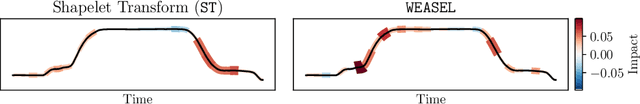
Modern time series classifiers display impressive predictive capabilities, yet their decision-making processes mostly remain black boxes to the user. At the same time, model-agnostic explainers, such as the recently proposed SHAP, promise to make the predictions of machine learning models interpretable, provided there are well-designed domain mappings. We bring both worlds together in our timeXplain framework, extending the reach of explainable artificial intelligence to time series classification and value prediction. We present novel domain mappings for the time and the frequency domain as well as series statistics and analyze their explicative power as well as their limits. We employ timeXplain in a large-scale experimental comparison of several state-of-the-art time series classifiers and discover similarities between seemingly distinct classification concepts such as residual neural networks and elastic ensembles.

Non-Monotone Submodular Maximization with Multiple Knapsacks in Static and Dynamic Settings

We study the problem of maximizing a non-monotone submodular function under multiple knapsack constraints. We propose a simple discrete greedy algorithm to approach this problem, and prove that it yields strong approximation guarantees for functions with bounded curvature. In contrast to other heuristics, this requires no problem relaxation to continuous domains and it maintains a constant-factor approximation guarantee in the problem size. In the case of a single knapsack, our analysis suggests that the standard greedy can be used in non-monotone settings. Additionally, we study this problem in a dynamic setting, by which knapsacks change during the optimization process. We modify our greedy algorithm to avoid a complete restart at each constraint update. This modification retains the approximation guarantees of the static case. We evaluate our results experimentally on a video summarization and sensor placement task. We show that our proposed algorithm competes with the state-of-the-art in static settings. Furthermore, we show that in dynamic settings with tight computational time budget, our modified greedy yields significant improvements over starting the greedy from scratch, in terms of the solution quality achieved.