Fair Correlation Clustering in Forests

The study of algorithmic fairness received growing attention recently. This stems from the awareness that bias in the input data for machine learning systems may result in discriminatory outputs. For clustering tasks, one of the most central notions of fairness is the formalization by Chierichetti, Kumar, Lattanzi, and Vassilvitskii [NeurIPS 2017]. A clustering is said to be fair, if each cluster has the same distribution of manifestations of a sensitive attribute as the whole input set. This is motivated by various applications where the objects to be clustered have sensitive attributes that should not be over- or underrepresented. We discuss the applicability of this fairness notion to Correlation Clustering. The existing literature on the resulting Fair Correlation Clustering problem either presents approximation algorithms with poor approximation guarantees or severely limits the possible distributions of the sensitive attribute (often only two manifestations with a 1:1 ratio are considered). Our goal is to understand if there is hope for better results in between these two extremes. To this end, we consider restricted graph classes which allow us to characterize the distributions of sensitive attributes for which this form of fairness is tractable from a complexity point of view. While existing work on Fair Correlation Clustering gives approximation algorithms, we focus on exact solutions and investigate whether there are efficiently solvable instances. The unfair version of Correlation Clustering is trivial on forests, but adding fairness creates a surprisingly rich picture of complexities. We give an overview of the distributions and types of forests where Fair Correlation Clustering turns from tractable to intractable. The most surprising insight to us is the fact that the cause of the hardness of Fair Correlation Clustering is not the strictness of the fairness condition.

timeXplain -- A Framework for Explaining the Predictions of Time Series Classifiers

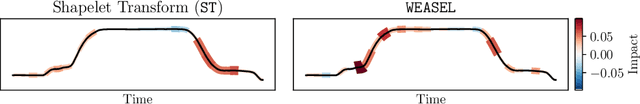
Modern time series classifiers display impressive predictive capabilities, yet their decision-making processes mostly remain black boxes to the user. At the same time, model-agnostic explainers, such as the recently proposed SHAP, promise to make the predictions of machine learning models interpretable, provided there are well-designed domain mappings. We bring both worlds together in our timeXplain framework, extending the reach of explainable artificial intelligence to time series classification and value prediction. We present novel domain mappings for the time and the frequency domain as well as series statistics and analyze their explicative power as well as their limits. We employ timeXplain in a large-scale experimental comparison of several state-of-the-art time series classifiers and discover similarities between seemingly distinct classification concepts such as residual neural networks and elastic ensembles.