Neural Gaussian Scale-Space Fields

Gaussian scale spaces are a cornerstone of signal representation and processing, with applications in filtering, multiscale analysis, anti-aliasing, and many more. However, obtaining such a scale space is costly and cumbersome, in particular for continuous representations such as neural fields. We present an efficient and lightweight method to learn the fully continuous, anisotropic Gaussian scale space of an arbitrary signal. Based on Fourier feature modulation and Lipschitz bounding, our approach is trained self-supervised, i.e., training does not require any manual filtering. Our neural Gaussian scale-space fields faithfully capture multiscale representations across a broad range of modalities, and support a diverse set of applications. These include images, geometry, light-stage data, texture anti-aliasing, and multiscale optimization.

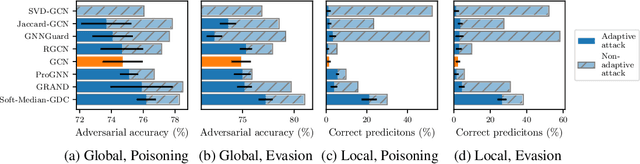
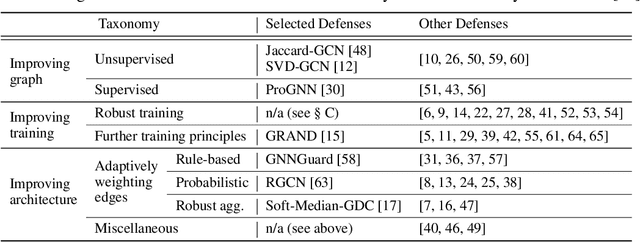
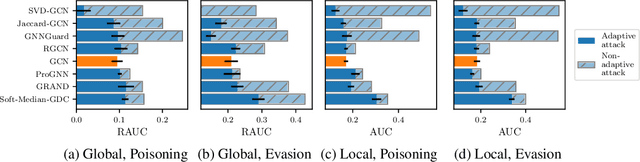
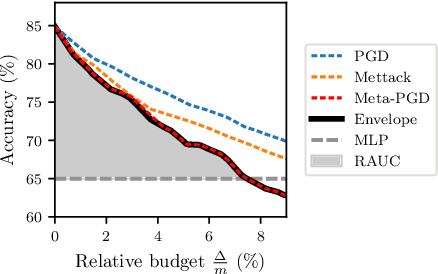
Are Defenses for Graph Neural Networks Robust?

A cursory reading of the literature suggests that we have made a lot of progress in designing effective adversarial defenses for Graph Neural Networks (GNNs). Yet, the standard methodology has a serious flaw - virtually all of the defenses are evaluated against non-adaptive attacks leading to overly optimistic robustness estimates. We perform a thorough robustness analysis of 7 of the most popular defenses spanning the entire spectrum of strategies, i.e., aimed at improving the graph, the architecture, or the training. The results are sobering - most defenses show no or only marginal improvement compared to an undefended baseline. We advocate using custom adaptive attacks as a gold standard and we outline the lessons we learned from successfully designing such attacks. Moreover, our diverse collection of perturbed graphs forms a (black-box) unit test offering a first glance at a model's robustness.

timeXplain -- A Framework for Explaining the Predictions of Time Series Classifiers

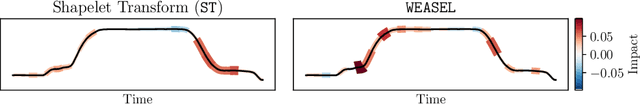
Modern time series classifiers display impressive predictive capabilities, yet their decision-making processes mostly remain black boxes to the user. At the same time, model-agnostic explainers, such as the recently proposed SHAP, promise to make the predictions of machine learning models interpretable, provided there are well-designed domain mappings. We bring both worlds together in our timeXplain framework, extending the reach of explainable artificial intelligence to time series classification and value prediction. We present novel domain mappings for the time and the frequency domain as well as series statistics and analyze their explicative power as well as their limits. We employ timeXplain in a large-scale experimental comparison of several state-of-the-art time series classifiers and discover similarities between seemingly distinct classification concepts such as residual neural networks and elastic ensembles.