Plus Strategies are Exponentially Slower for Planted Optima of Random Height

We compare the $(1,\lambda)$-EA and the $(1 + \lambda)$-EA on the recently introduced benchmark DisOM, which is the OneMax function with randomly planted local optima. Previous work showed that if all local optima have the same relative height, then the plus strategy never loses more than a factor $O(n\log n)$ compared to the comma strategy. Here we show that even small random fluctuations in the heights of the local optima have a devastating effect for the plus strategy and lead to super-polynomial runtimes. On the other hand, due to their ability to escape local optima, comma strategies are unaffected by the height of the local optima and remain efficient. Our results hold for a broad class of possible distortions and show that the plus strategy, but not the comma strategy, is generally deceived by sparse unstructured fluctuations of a smooth landscape.

Maps for Learning Indexable Classes

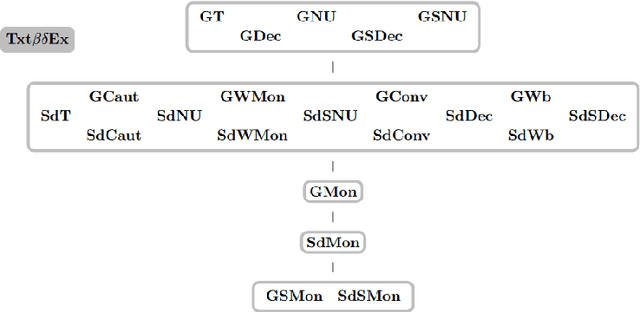
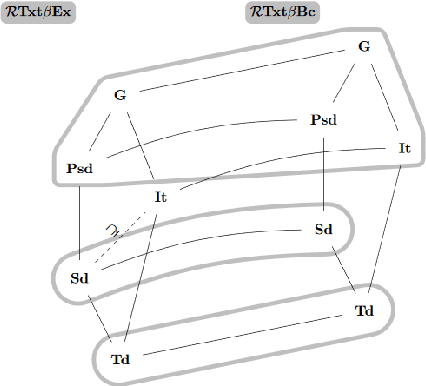
We study learning of indexed families from positive data where a learner can freely choose a hypothesis space (with uniformly decidable membership) comprising at least the languages to be learned. This abstracts a very universal learning task which can be found in many areas, for example learning of (subsets of) regular languages or learning of natural languages. We are interested in various restrictions on learning, such as consistency, conservativeness or set-drivenness, exemplifying various natural learning restrictions. Building on previous results from the literature, we provide several maps (depictions of all pairwise relations) of various groups of learning criteria, including a map for monotonicity restrictions and similar criteria and a map for restrictions on data presentation. Furthermore, we consider, for various learning criteria, whether learners can be assumed consistent.